Método dos Elementos Finitos
Abordagens para simulaçoes não-lineares
Prof. Marco André Argenta / PPGECC / UFPR
Objetivos da disciplina
Objetivos da disciplina
- Entender o que é um problema não linear estrutural.
- O que difere uma solução linear ou uma solução não linear de uma estrutura.
- Tipos de não linearidade.
- Tensões e deformações em estruturas com respostas não lineares.
- Formulação de problemas de estruturas não lineares.
- Solução das equações de problemas de estruturas não lineares.
- Dificuldade na solução e modelagem para estruturas não linear.
Simulação não linear de estruturas
O que é um comportamento não linear de uma estrutura?
- É a não existência de proporcionalidade entre quaisquer ou várias grandezas estruturais.
O que é um comportamento linear?
- É justamente a EXISTÊNCIA OBRIGATÓRIA de proporcionalidade entre TODAS as grandezas estruturais!
Simulação linear de estruturas
A linearidade é uma aproximação:
- Pequenas deformações (<0,2%)
- Pequenos deslocamentos
- Pequenas rotações
- Relações constitutivas tensão-deformação linear
- Condições de contorno constantes
- Forças aplicadas constantes*
Com proporcionalidade entre todas as grandezas!
Proporcionalidades:
Observação de problemas estruturais
Qual dos dois acontece na simulação linear? E na estrutura real?
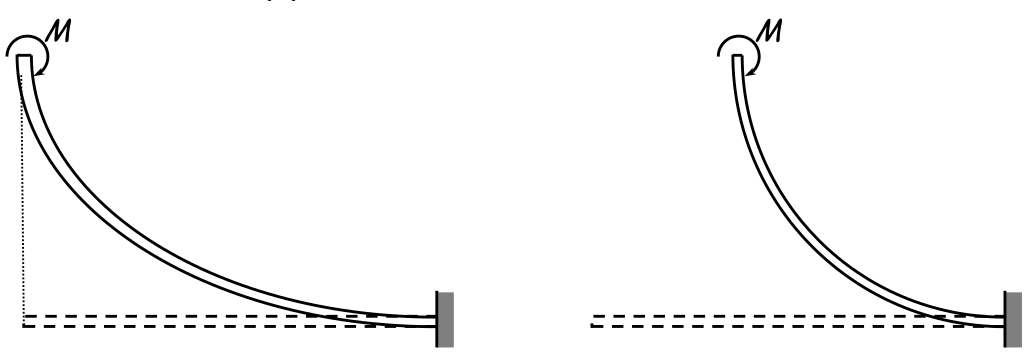
E isso? Acontece na linear?

Código para teste linear da viga
Equação diferencial da linha neutra: $$ E I_z \dfrac{d^2y}{dx^2}=-M $$
import numpy as np
import matplotlib.pyplot as plt
M = 10 #kNm
Iz = 0.000533 #m4
E = 200000000 #kN/m2
l = 2 #m
def func(x):
return -M*x**2/(2*E*Iz)
x = np.linspace(0, 2, 10)
y = func(x)
plt.plot(x, y, 'r', linewidth=2)
plt.xlim(xmin=0, xmax=2.2)
plt.show()
Código para teste não linear da viga
Equação diferencial da linha neutra: $$ \dfrac{\dfrac{d^2y}{dx^2}}{\left[ 1 + \left( \dfrac{dy}{dx} \right)^2 \right]^{\frac{3}{2}}} = \dfrac{M}{EI} $$
import numpy as np
import matplotlib.pyplot as plt
?????
Não linearidade em estruturas
Tipos de não linearidade em estruturas
- Não linearidade geométrica: relação deformação-deslocamento não linear;
- Não linearidade material: relação constitutiva não linear;
- Não linearidade cinemática: condições de contorno ou apoios não constantes
- Não linearidade da força: forças aplicadas dependem da configuração do corpo (efeitos de segunda ordem).
Mais de uma não linearidade pode existir ao mesmo tempo!
Não linearidade geométrica
Relações entre quantidades cinemáticas (ou seja, deslocamento, rotação e deformações) são não linear*
Relação deslocamento-deformação:
Não linearidade geométrica (cont.)
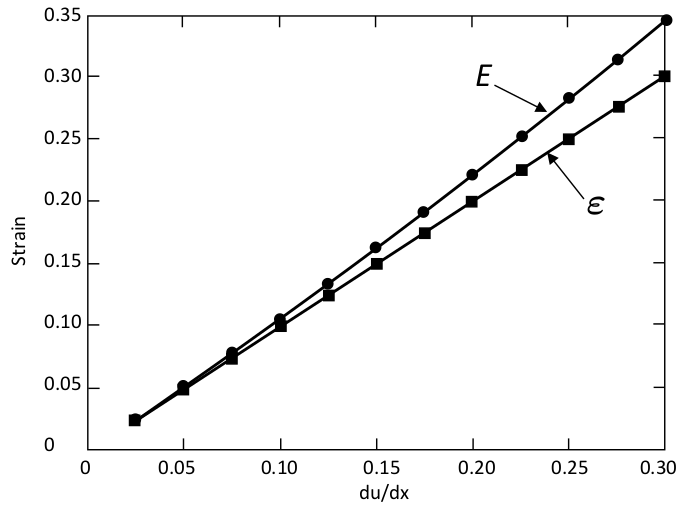
- $\varXi(x)$ tem um termo de alta ordem;
- $ \dfrac{du}{dx} \ll 1 \rightarrow \varepsilon(x) \sim \varXi(x) $
- Domínio $ \Omega_0 $ indeformado;
- Domínio deformado $ \Omega_x $
Não linearidade material
Material no regime elástico linear:
$$ \sigma = D \varepsilon $$ $$ U = \dfrac{1}{2} E \varepsilon^2 \quad \text{e} \quad \sigma = \dfrac{dU}{d \varepsilon}=E \varepsilon $$- Somente para deformações infinitesimais!
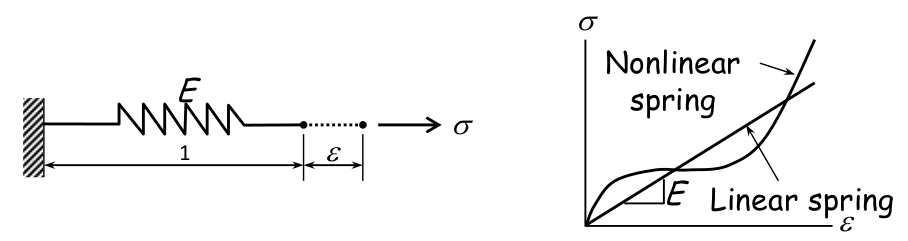
Material com comportamento não linear elástico:
$$ \sigma = f(\varepsilon) $$- $ D $ não é constante e depende da deformação;
- A tensão é uma função da deformação.
Não linearidade material (cont. 1)
Material elastoplastico (dissipação de energia):
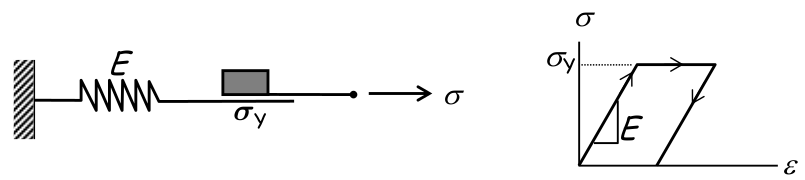
- Suporta tensões até $\sigma_y$;
- A tensão não pode ser determinada apenas pela tensão em si;
- O histórico de carregamento é necessário: "path-dependent".
Não linearidade material (cont. 2)
Material viscoelástico:
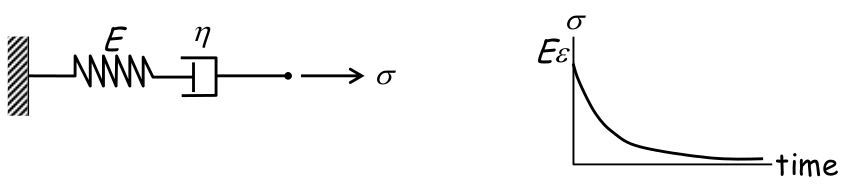
- Comportamento dependente do tempo;
- Fluência, relaxação.
Não linearidade cinemática
Condição de contorno ou borda não linear
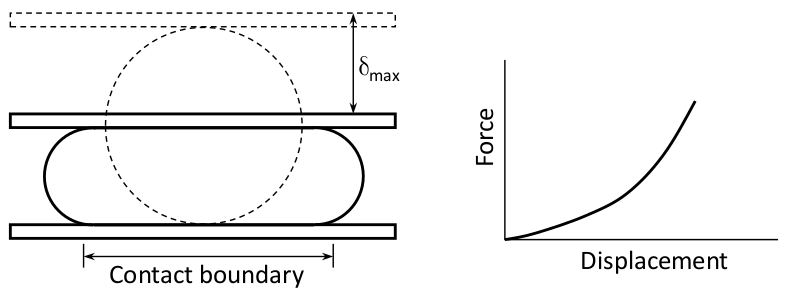
Problemas de contato, condições de apoio deslocáveis ou dependente de deslocamentos
Não linearidade da força
Cargas aplicadas não lineares

Aplicação da força depende da deformada do corpo (efeitos de segunda ordem)
Cargas de pressão de fluídos, carga excêntrica no topo de pilares...
Identifique as Não linearidades do processo
Não linearidades simples e complicadas
Simples:
- Relações contínuas não lineares tensão-deformação não dependentes do histórico de carregamento;
- Elasticidade não linear, não linearidade geométrica e cargas dependentes da deformação.
Complicadas:
- Relações não lineares tensão-deformação dependentes do histórico de carregamento;
- Elastoplasticidade e problemas de contato.
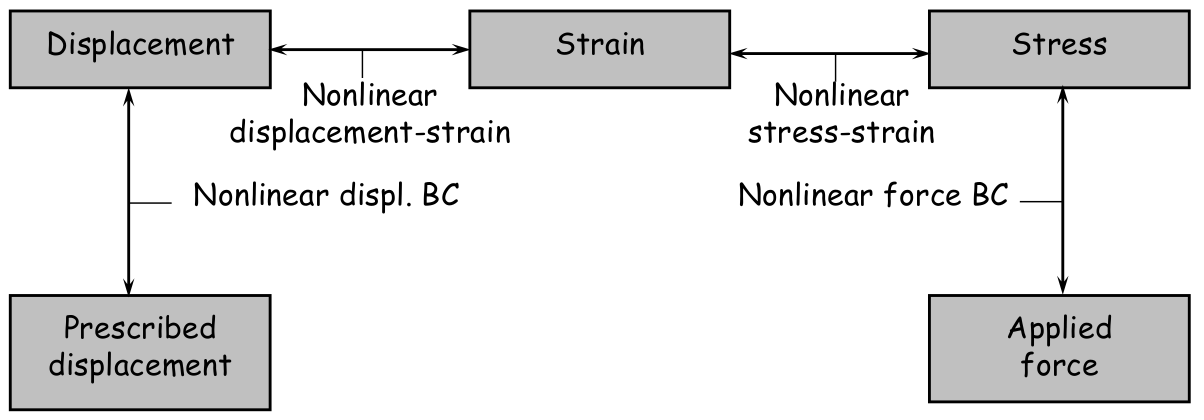
Equações Não lineares de Elementos Finitos
Equilíbrio entre forças internas e externas
$$ P(d) = F(d) $$Não linearidades cinética e cinemática:
- Aparecem nos contornos;
- Governadas por deslocamentos e forças (global, explícita).
Não linearidades geométrica e de material (física):
- Aparecem no domíno;
- Dependem de tensões e deformações (locais, implícitas).
Procedimento de Solução
Procedimento de Solução
Somente se resolvem problemas lineares...
Exemplo: Molas não lineares

Rigidez das molas:
$$ k_1 = 50 + 500u $$ $$ k_2 = 100 + 200u $$Equações governantes:
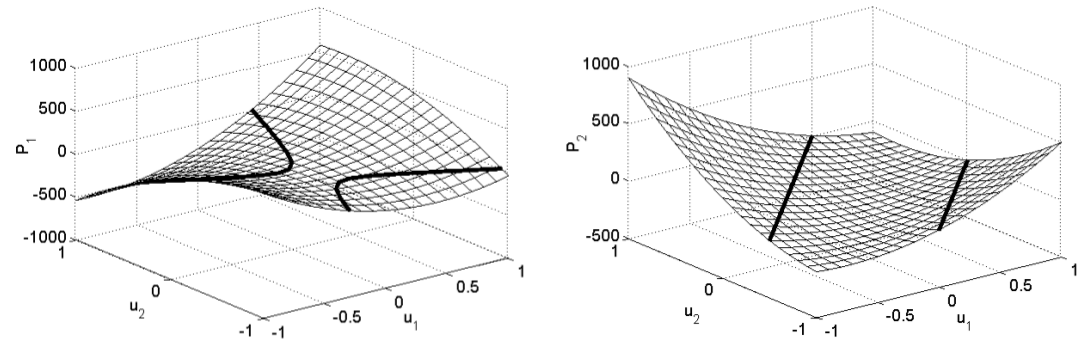
$$ \begin{cases} 300u_1^2 + 400u_1u_2 - 200u_2^2 + 150u_1 - 100 u_2 = 0 \\ 200u_1^2 - 400u_1u_2 + 200u_2^2 - 100u_1 + 100 u_2 = 100 \end{cases} $$Exemplo: Molas não lineares (cont.)
- A solução são as curvas de intersecção entre os planos das equações governantes (P1 primeira, P2 segunda);
- Multiplas soluções podem existir;
- Em certa situação, nenhuma solução existe.
Procedimento de Solução
Problemas lineares
A matriz de rigidez K é constante
$$ P(d_1 + d_2) = P(d_1) + P(d_2) $$ $$ P(\alpha d) = \alpha P(d) = \alpha F $$- Se a carga dobra, o deslocamento dobra;
- Superposição dos efeitos é possível!.

Procedimento de Solução (cont.)
Problemas não lineares
- Como achar d para uma dada F?
Procedimento incremental de solução!
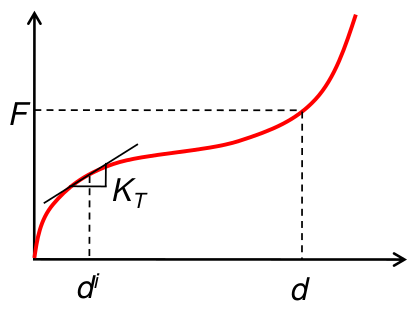
Método de Newton-Raphson
- Método mais popular;
- Equações não lineares são aproximadas por equações locais lineares iterativamente até satisfazerem certa tolerância;
- Estima-se $ d^i $ da i-ésima iteração;
- Calcula-se $ d^{i+1} $ a partir de uma expansão em séries de Taylor de primeira ordem:
Método de Newton-Raphson (cont. 1)
- Resolve-se a solução incremental:
- Atualiza-se a solução:
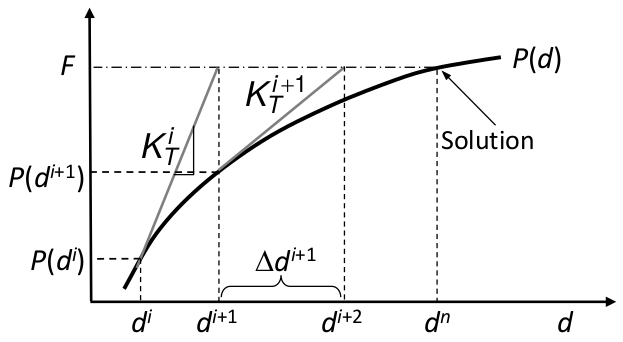
Método de Newton-Raphson (cont. 2)
Observações:
- A solução converge rapidamente quando a estimativa inicial está próxima da solução;
- Quanto a iteração atual está próxima da solução, o método apresenta convergência de segunda ordem (rápido)*;
- Rigidez Tangente $ K_T^i(d^i) $ não é constante;
- A equação matricial é resolvida para deslocamentos incrementais $ \Delta d^i $;
Método de Newton-Raphson (cont. 3)
Observações:
- O lado direito da equação não representa uma força, mas sim uma força residual:
- As iterações param quando é satisfeita certa tolerância:
Algoritmo de Newton-Raphson
INÍCIO:Definir a tolerância ($tol = 10^{-3}$), $i = 0$, $max_{iter} = 20$ e estimar $d = d^0$.
- Calcular a força residual: $R^i \equiv F - P(d^i)$ e se $conv_F \leq tol_F$, cálculo completo!
- Calcular a matriz Jacobiana, ou rigidez tangente $ K_T^i $;
- Se o determinante de $ K_T $ for zero, pare com mensagem de erro!
- Calcular o incremento da solução $ K_T^i \Delta d^i = F - P(d^i) $ e se $conv_d \leq tol_d$, cálculo completo!
- Atualizar a solução: $ d^{i+1} = d^i + \Delta d^i $
- Definir: $ i = i + 1 $ e se $ i > max_{iter} $, pare com mensagem de erro!
- Ou então, voltar ao passo 1!
Exemplo do método de Newton-Raphson
Seja o sistema não linear: $$ P(d) = F \quad \Rightarrow \quad \begin{Bmatrix} d_1 + d_2 \\ d_1^2 + d_2^2 \end{Bmatrix} = \begin{Bmatrix} 3 \\ 9 \end{Bmatrix} $$Solução usando Newton-Raphson:
INÍCIO: Arbitrando inicialmente a tolerância ($tol = 10^{-3}$), $i = 0$, $max_{iter} = 20$, estimando $ d = d^0 = \begin{Bmatrix} 1 \\ 5 \end{Bmatrix} \ \rightarrow \ P(d^0) = \begin{Bmatrix} 6 \\ 26 \end{Bmatrix}$ e a matriz Jacobiana (ou rigidez tangente): $ K_T^i(d^i) \equiv \left( \dfrac{\partial P}{\partial d} \right)^i = \begin{bmatrix} \frac{\partial P_1}{\partial d_1} & \frac{\partial P_1}{\partial d_2} \\ \frac{\partial P_2}{\partial d_1} & \frac{\partial P_2}{\partial d_2} \end{bmatrix}^i = \begin{bmatrix} 1 & 1 \\ 2 d_1^i & 2 d_2^i \end{bmatrix}^i$Exemplo MN-R (cont. 1)
1. Calculando a força residual: $ R^0 = F - P(d^0) = \begin{Bmatrix}
-3 \\
-17
\end{Bmatrix}$
Verificando a convergência da força residual:
$ conv_F = \dfrac{\sum_{j=1}^{n} \left( R_j^{i} \right)^2}{1 + \sum_{j=1}^{n} \left( F_j \right)^2} =
\dfrac{\left(R_1^{0}\right)^2 + \left(R_2^{0}\right)^2 }{1 +\left(F_1\right)^2 + \left(F_2\right)^2} =
\dfrac{\left[ (-3)^2 + (-17)^2 \right]}{1 +\left( 3^2 + 9^2 \right)} = 2,7586 $
$ \therefore conv_F = 3,2747 > tol = 10^{-3} $ continua...
2. Calculando a matriz Jacobiana (ou rigidez tangente): $ K_T^0 = \begin{bmatrix}
1 & 1 \\
2 & 10
\end{bmatrix}^0$
Verificando o determinante de $ K_T^0 $: $ det(K_T^0) = 8 \neq 0$ OK!
Exemplo MN-R (cont. 2)
3. Calculando o incremento da solução: $ K_T^0 \Delta d^0 = R^0 = \begin{bmatrix} 1 & 1 \\ 2 & 10 \end{bmatrix}^0 \begin{Bmatrix} \Delta d_1^0 \\ \Delta d_2^0 \end{Bmatrix} = \begin{Bmatrix} -3 \\ -17 \end{Bmatrix}$$ \therefore \begin{Bmatrix} \Delta d_1^0 \\ \Delta d_2^0 \end{Bmatrix} = \begin{Bmatrix} -1,625 \\ -1,375 \end{Bmatrix} $
Verificando a convergência dos incrementos de deslocamentos: $conv_d = \dfrac{\sum_{j=1}^{n} \left( \Delta d_j^{i} \right)^2}{1 + \sum_{j=1}^{n} \left( \Delta d_j^0 \right)^2} = \dfrac{\left[ (-1,625)^2 + (-1,375)^2 \right]}{1 + \left[ (-1,625)^2 + (-1,375)^2 \right]} = 0,8192 $
$\therefore conv_d = 0,8192 > tol = 10^{-3} $ continua...
Exemplo MN-R (cont. 3)
4. Atualizando a solução: $ d^1 = d^0 + \Delta d^0 = \begin{Bmatrix} -0,625 \\ 3,625 \end{Bmatrix}$
5. Atualizando $i$: $i = i + 1 \quad i = 0 + 1 = 1$
Verificando o número de passos: $ i < max_{iter} \quad \therefore i = 1 < 20$ OK!
Inicia-se nova iteração!
Exemplo MN-R (cont. 4)
1. Calculando a força residual: $ R^1 = F - P(d^1) = \begin{Bmatrix}
0 \\
-4,531
\end{Bmatrix}$
Verificando a convergência da força residual:
$ conv_F = \dfrac{\sum_{j=1}^{n} \left( R_j^{i} \right)^2}{1 + \sum_{j=1}^{n} \left( F_j \right)^2} =
\dfrac{\left[ 0^2 + (-4,531)^2 \right]}{1 +\left( 3^2 + 9^2 \right)} = 0,2256 $
$ \therefore conv_F = 0,2256 > tol = 10^{-3} $ continua...
2. Calculando a matriz Jacobiana (ou rigidez tangente): $ K_T^1 = \begin{bmatrix}
1 & 1 \\
-1,25 & 7,25
\end{bmatrix}^1$
Verificando o determinante de $ K_T^1 $: $ det(K_T^1) = 8,5 \neq 0$ OK!
Exemplo MN-R (cont. 5)
3. Calculando o incremento da solução: $ K_T^1 \Delta d^1 = R^1 = \begin{bmatrix} 1 & 1 \\ -1,25 & 7,25 \end{bmatrix}^0 \begin{Bmatrix} \Delta d_1^1 \\ \Delta d_2^1 \end{Bmatrix} = \begin{Bmatrix} 0 \\ -4,531 \end{Bmatrix}$$ \therefore \begin{Bmatrix} \Delta d_1^1 \\ \Delta d_2^1 \end{Bmatrix} = \begin{Bmatrix} 0,533 \\ -0,533 \end{Bmatrix} $
Verificando a convergência dos incrementos de deslocamentos: $conv_d = \dfrac{\sum_{j=1}^{n} \left( \Delta d_j^{i} \right)^2}{1 + \sum_{j=1}^{n} \left( \Delta d_j^0 \right)^2} = \dfrac{\left[ (0,533)^2 + (-0,533)^2 \right]}{1 + \left[ (-1,625)^2 + (-1,375)^2 \right]} = 0,10272 $
$\therefore conv_d = 0,10272 > tol = 10^{-3} $ continua...
Exemplo MN-R (cont. 6)
4. Atualizando a solução: $ d^2 = d^1 + \Delta d^1 = \begin{Bmatrix} -0,092 \\ 3,092 \end{Bmatrix}$
5. Atualizando $i$: $i = i + 1 \quad i = 1 + 1 = 2$
Verificando o número de passos: $ i < max_{iter} \quad \therefore i = 2 < 20$ OK!
Inicia-se nova iteração!
Exemplo MN-R (cont. 7)
1. Calculando a força residual: $ R^2 = F - P(d^2) = \begin{Bmatrix}
0 \\
-0,568
\end{Bmatrix}$
Verificando a convergência da força residual:
$ conv_F = \dfrac{\sum_{j=1}^{n} \left( R_j^{i} \right)^2}{1 + \sum_{j=1}^{n} \left( F_j \right)^2} =
\dfrac{\left[ 0^2 + (-0,568)^2 \right]}{1 +\left( 3^2 + 9^2 \right)} = 0,003545 $
$ \therefore conv_F = 0,003545 > tol = 10^{-3} $ continua...
2. Calculando a matriz Jacobiana (ou rigidez tangente): $ K_T^2 = \begin{bmatrix}
1 & 1 \\
-0,184 & 6,184
\end{bmatrix}^1$
Verificando o determinante de $ K_T^2 $: $ det(K_T^2) = 6,368 \neq 0$ OK!
Exemplo MN-R (cont. 8)
3. Calculando o incremento da solução: $ K_T^2 \Delta d^2 = R^2 = \begin{bmatrix} 1 & 1 \\ -0,184 & 6,184 \end{bmatrix}^0 \begin{Bmatrix} \Delta d_1^2 \\ \Delta d_2^2 \end{Bmatrix} = \begin{Bmatrix} 0 \\ -0,568 \end{Bmatrix}$$ \therefore \begin{Bmatrix} \Delta d_1^2 \\ \Delta d_2^2 \end{Bmatrix} = \begin{Bmatrix} 0,089 \\ -0,089 \end{Bmatrix} $
Verificando a convergência dos incrementos de deslocamentos: $conv_d = \dfrac{\sum_{j=1}^{n} \left( \Delta d_j^{i} \right)^2}{1 + \sum_{j=1}^{n} \left( \Delta d_j^0 \right)^2} = \dfrac{\left[ (0,089)^2 + (-0,089)^2 \right]}{1 + \left[ (-1,625)^2 + (-1,375)^2 \right]} = 0,002864 $
$\therefore conv_d = 0,002864 > tol = 10^{-3} $ continua...
Exemplo MN-R (cont. 9)
4. Atualizando a solução: $ d^3 = d^2 + \Delta d^2 = \begin{Bmatrix} -0,003 \\ 3,003 \end{Bmatrix}$
5. Atualizando $i$: $i = i + 1 \quad i = 2 + 1 = 3$
Verificando o número de passos: $ i < max_{iter} \quad \therefore i = 3 < 20$ OK!
Inicia-se nova iteração!
Exemplo MN-R (cont. 10)
1. Calculando a força residual: $ R^3 = F - P(d^3) = \begin{Bmatrix}
0 \\
-0,016
\end{Bmatrix}$
Verificando a convergência da força residual:
$ conv_F = \dfrac{\sum_{j=1}^{n} \left( R_j^{i} \right)^2}{1 + \sum_{j=1}^{n} \left( F_j \right)^2} =
\dfrac{\left[ 0^2 + (-0,016)^2 \right]}{1 +\left( 3^2 + 9^2 \right)} = 0,000002535 $
$ \therefore conv_F = 0,000002535 < tol = 10^{-3} $ CÁLCULO ENCERRADO!
2. Calculando a matriz Jacobiana (ou rigidez tangente): $ K_T^3 = \begin{bmatrix}
1 & 1 \\
-0,005 & 6,005
\end{bmatrix}^1$
Verificando o determinante de $ K_T^2 $: $ det(K_T^2) = 6,01 \neq 0$ OK!
Exemplo MN-R (cont. 11)
3. Calculando o incremento da solução: $ K_T^3 \Delta d^3 = R^3 = \begin{bmatrix} 1 & 1 \\ -0,005 & 6,005 \end{bmatrix}^0 \begin{Bmatrix} \Delta d_1^3 \\ \Delta d_2^3 \end{Bmatrix} = \begin{Bmatrix} 0 \\ -0,016 \end{Bmatrix}$$ \therefore \begin{Bmatrix} \Delta d_1^3 \\ \Delta d_2^3 \end{Bmatrix} = \begin{Bmatrix} 0,003 \\ -0,003 \end{Bmatrix} $
Verificando a convergência dos incrementos de deslocamentos: $conv_d = \dfrac{\sum_{j=1}^{n} \left( \Delta d_j^{i} \right)^2}{1 + \sum_{j=1}^{n} \left( \Delta d_j^0 \right)^2} = \dfrac{\left[ (0,003)^2 + (-0,003)^2 \right]}{1 + \left[ (-1,625)^2 + (-1,375)^2 \right]} = 0,000005137 $
$\therefore conv_d = 0,000005137 < tol = 10^{-3} $ CÁLCULO ENCERRADO!
Exemplo MN-R (cont. 12)
4. Atualizando a solução: $ d^4 = d^3 + \Delta d^3 = \begin{Bmatrix} -0,003 \\ 3,000 \end{Bmatrix}$
5. Atualizando $i$: $i = i + 1 \quad i = 3 + 1 = 4$
Verificando o número de passos: $ i < max_{iter} \quad \therefore i = 4 < 20$ OK!
Não precisa de nova iteração!
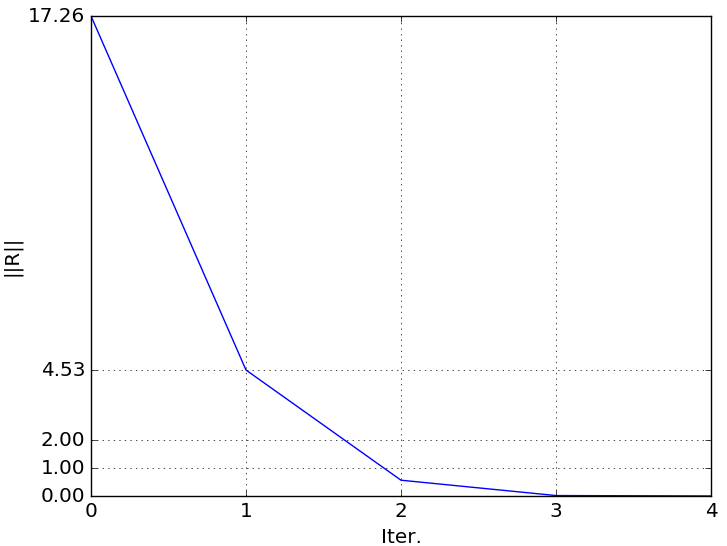

Quando Newton-Raphson não converge
Dificuldades:
- A convergência não é sempre garantida! A solução pode divergir;
- Controle automático de passo de carga e/ou técnicas de busca linear são usados frequentemente;
- Cálculo difícil ou dispendioso de $ K_T^I(d^i) $;
- A solução pode oscilar entre dois pontos.

Quando Newton-Raphson não converge (cont.)
Dificuldades na convergência ocorrem quando:
- A matriz Jacobiana (ou de rigidez tangente) não é positivo-definida*;
- Bifurcações e salto por instabilidade (snap-through)** exigem um algoritmo especial.
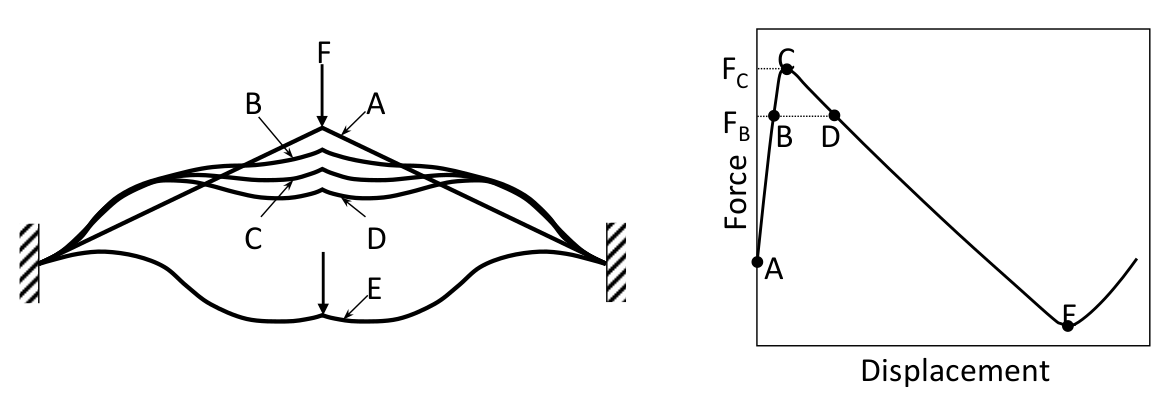
Exercícios
1. Resolver as molas não lineares em série usando Newton-Raphson:

Rigidez das molas:
$$ k_1 = 50 + 500u $$ $$ k_2 = 100 + 200u $$Equações governantes:
$$ \begin{cases} 300u_1^2 + 400u_1u_2 - 200u_2^2 + 150u_1 - 100 u_2 = 0 \\ 200u_1^2 - 400u_1u_2 + 200u_2^2 - 100u_1 + 100 u_2 = 100 \end{cases} $$2. Resolver a seguinte equação não linear usando Newton-Raphson:
$$ P(u) = u + tan^{-1}(5u) $$*Use como tolerância $ 10^{-5} $ e como estimativa inicial $ u^0 = 0,5 $
Método de Newton-Raphson Modificado
- Construir $ K_T^i(d^i) $ e resolver $ K_T^i \Delta d^i = R^i $ é custoso;
- Custo computacional (matriz de tamanho NxN):
- Decomposição LU ~ $ N^2 $
- Substituição Progressiva/Inversa ~ N
Usa-se, então, a decomposição LU em $ K_T^i(d^i) $ repetidamente*.
É mais estável que o método de Newton-Raphson.
É possível formular um método híbrido**.

Algoritmo de Newton-Raphson Modificado
INÍCIO:Definir a tolerância ($tol = 10^{-3}$), $i = 0$, $max_{iter} = 20$ e estimar $d = d^0$.
Calcular a matriz Jacobiana, ou rigidez tangente $ K_T^i $:
- Se o determinante de $ K_T $ for zero, pare com mensagem de erro!
- Se não, calcule a inversa $ \left( K_T^i \right)^{-1} $
- Calcular a força residual: $R^i \equiv F - P(d^i)$ e se $conv_F \leq tol_F$, cálculo completo!
- Calcular o incremento da solução $ \Delta d^i = \left( K_T^i \right)^{-1} \left[ F - P(d^i) \right] $ e se $conv_d \leq tol_d$, cálculo completo!
- Atualizar a solução: $ d^{i+1} = d^i + \Delta d^i $
- Definir: $ i = i + 1 $ e se $ i > max_{iter} $, pare com mensagem de erro!
- Ou então, voltar ao passo 1!
Exemplo do método de Newton-Raphson Modificado
Resolver o mesmo sistema não linear com o método de Newton-Raphson Modificado: $$ P(d) = F \quad \Rightarrow \quad \begin{Bmatrix} d_1 + d_2 \\ d_1^2 + d_2^2 \end{Bmatrix} = \begin{Bmatrix} 3 \\ 9 \end{Bmatrix} $$Solução usando Newton-Raphson:
INÍCIO: Arbitrando inicialmente a tolerância ($tol = 10^{-3}$), $i = 0$, $max_{iter} = 20$, estimando $ d = d^0 = \begin{Bmatrix} 1 \\ 5 \end{Bmatrix} \ \rightarrow \ P(d^0) = \begin{Bmatrix} 6 \\ 26 \end{Bmatrix}$ e a matriz Jacobiana (ou rigidez tangente): $ K_T^i(d^i) \equiv \left( \dfrac{\partial P}{\partial d} \right)^i = \begin{bmatrix} \frac{\partial P_1}{\partial d_1} & \frac{\partial P_1}{\partial d_2} \\ \frac{\partial P_2}{\partial d_1} & \frac{\partial P_2}{\partial d_2} \end{bmatrix}^i = \begin{bmatrix} 1 & 1 \\ 2 d_1^i & 2 d_2^i \end{bmatrix}^i \ \therefore K_T^0 = \begin{bmatrix} 1 & 1 \\ 2 & 10 \end{bmatrix}$Exemplo MN-RM (cont. 1)
Verificando o determinante de $ K_T^0 $: $ det(K_T^0) = 8 \neq 0$ OK!
Calculando a inversa da matriz Jacobiana (ou rigidez tangente):
$ \left(K_T^0\right)^{-1} = \begin{bmatrix}
1,25 & -0,125 \\
-0,25 & 0,125
\end{bmatrix}$
1. Calculando a força residual: $ R^0 = F - P(d^0) = \begin{Bmatrix}
-3 \\
-17
\end{Bmatrix}$
Verificando a convergência da força residual:
$ conv_F = \dfrac{\sum_{j=1}^{n} \left( R_j^{i} \right)^2}{1 + \sum_{j=1}^{n} \left( F_j \right)^2} =
\dfrac{\left(R_1^{0}\right)^2 + \left(R_2^{0}\right)^2 }{1 +\left(F_1\right)^2 + \left(F_2\right)^2} =
\dfrac{\left[ (-3)^2 + (-17)^2 \right]}{1 +\left( 3^2 + 9^2 \right)} = 2,7586 $
$ \therefore conv_F = 3,2747 > tol = 10^{-3} $ continua...
Exemplo MN-RM (cont. 2)
2. Calculando o incremento da solução: $ \Delta d^0 = \left(K_T^0\right)^{-1} R^0 = \begin{Bmatrix} \Delta d_1^0 \\ \Delta d_2^0 \end{Bmatrix} = \begin{bmatrix} 1,25 & -0,125 \\ -0,25 & 0,125 \end{bmatrix} \begin{Bmatrix} -3 \\ -17 \end{Bmatrix}$$ \therefore \begin{Bmatrix} \Delta d_1^0 \\ \Delta d_2^0 \end{Bmatrix} = \begin{Bmatrix} -1,625 \\ -1,375 \end{Bmatrix} $
Verificando a convergência dos incrementos de deslocamentos: $conv_d = \dfrac{\sum_{j=1}^{n} \left( \Delta d_j^{i} \right)^2}{1 + \sum_{j=1}^{n} \left( \Delta d_j^0 \right)^2} = \dfrac{\left[ (-1,625)^2 + (-1,375)^2 \right]}{1 + \left[ (-1,625)^2 + (-1,375)^2 \right]} = 0,8192 $
$\therefore conv_d = 0,8192 > tol = 10^{-3} $ continua...
Exemplo MN-RM (cont. 3)
3. Atualizando a solução: $ d^1 = d^0 + \Delta d^0 = \begin{Bmatrix} -0,625 \\ 3,625 \end{Bmatrix}$
4. Atualizando $i$: $i = i + 1 \quad i = 0 + 1 = 1$
Verificando o número de passos: $ i < max_{iter} \quad \therefore i = 1 < 20$ OK!
Inicia-se nova iteração!*
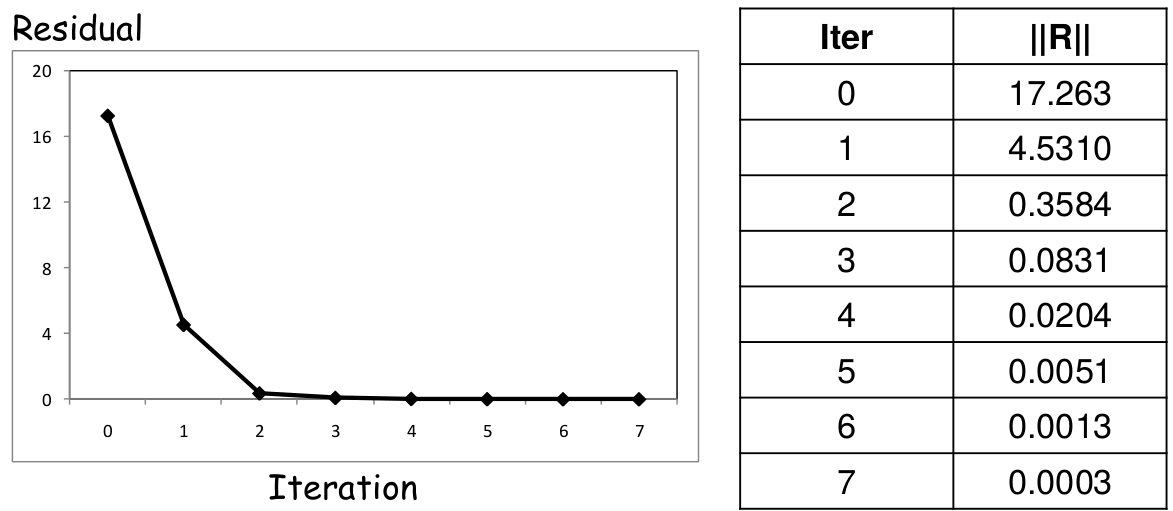
Exercícios
1. Resolver as mesmas molas não lineares em série usando Newton-Raphson Modificado*:

Rigidez das molas:
$$ k_1 = 50 + 500u $$ $$ k_2 = 100 + 200u $$Equações governantes:
$$ \begin{cases} 300u_1^2 + 400u_1u_2 - 200u_2^2 + 150u_1 - 100 u_2 = 0 \\ 200u_1^2 - 400u_1u_2 + 200u_2^2 - 100u_1 + 100 u_2 = 100 \end{cases} $$2. Resolver a mesma equação não linear usando Newton-Raphson Modificado:
$$ P(u) = u + tan^{-1}(5u) $$*Use como tolerância $ 10^{-5} $ e como estimativa inicial $ u^0 = 0,5 $
Método da Secante
Utiliza uma aproximação usando a iteração anterior no lugar do jacobiano (rigidez tangente);
Na i-ésima iteração:
$$ K_s^i \Delta d^i = F - P(d^i) $$A matriz secante satisfaz:
$$ K_s^i \left( d^i - d^{i-1} \right) = P(d^i) - P(d^{i-1}) $$Ou seja, o incremento de deslocamento é:
$$ \Delta d^i = \dfrac{d^i - d^{i-1}}{P(d^i) - P(d^{i-1})}\left[ F - P(d^i) \right] $$Para grandes dimensões não se torna um processo unicamente definido!

Método da Secante (cont. 1)
Inicia-se da matriz $ K_T $, idêntica ao método de Newton-Raphson,
sendo atualizada iterativamente.
O problema realmente é como fazer sua atualização!
A atualização pode ser feita por dois métodos:
- Algoritmo de Broyden (atualização da rigidez*);
- Método BFGS (Broyden, Fletcher, Goldfarb e Shanno, atualização da inversa da rigidez**).
Método da Secante - Broyden
A atualização da rigidez é feita com:
$$ K_s^i = K_s^{i-1} + \dfrac{\Delta R - K_s^{i-1} \Delta d}{\lVert \Delta d \rVert^2} \Delta d^T $$Sendo:
$$ \Delta R = R(d^i) - R(d^{i-1}) \quad \text{e} \quad \Delta d = d^i - d^{i-1} $$Então, resolve-se:
$$ K_s^i \Delta d^i = F - P(d^i) $$E, atualiza-se a solução com:
$$ d^{i+1} = d^i + \Delta d^i $$Método da Secante - O Algoritmo de Broyden
INÍCIO:Definir a tolerância ($tol = 10^{-3}$), $i = 0$, $max_{iter} = 20$ e estimar $d = d^0$.
Calcular a matriz Jacobiana, ou rigidez tangente $ K_T^i $:
- Definir, inicialmente, que $ K_s^0 \equiv K_T^0 $;
- Se $ det(K_s^0) = 0 $, pare com mensagem de erro!
- Se não, calcule $ \left( K_s^0 \right)^{-1} $;
- Calcular $ P(d^0) $ e $ R^0 = P(d^0) - F $;
Continuação - O Algoritmo de Broyden (iterações)
- Calcular o incremento da solução $ \Delta d^i = -\left( K_s^{i-1} \right)^{-1} R(d^{i-1}) $, sendo $ R(d^{i-1}) = \left[ P(d^{i-1} - F) \right] $ e se $conv_d \leq tol_d$, cálculo completo!
- Atualizar a solução: $ d^{i} = d^{i-1} + \Delta d^i $;
- Calcular $ R(d^i) = P(d^i) - F $ e se $conv_F \leq tol_F$, cálculo completo!;
- Calcular $ \Delta R = R(d^i) - R(d^{i-1}) $;
- Atualizar a rigidez secante: $ K_s^i = K_s^{i-1} + \dfrac{\Delta R - K_s^{i-1} \Delta d^i} {\lVert \Delta d^i \rVert^2} \left( \Delta d^i \right)^T $
- Se $ det(K_s^i) = 0 $, pare com mensagem de erro!
- Se não, calcule $ \left( K_s^i \right)^{-1} $;
- Definir: $ i = i + 1 $ e se $ i > max_{iter} $, pare com mensagem de erro!
- Ou então, voltar ao passo 1!
Método da Secante - Método BFGS
A atualização da inversa da rigidez $ \left(K_s^i\right)^{-1} \equiv H_s^i $ é feita com:
$$ H_s^i = \left[ I + w^i (v^i)^T \right] H_s^{i-1} \left[ I + w^i (v^i)^T \right] $$Sendo:
$$ v^i = R^{i-1} \left[ 1 - \dfrac{(\Delta d^{i-1})^T (R^{i-1} - R^i)}{(\Delta d^{i})^T R^{i-1}} \right] - R^i $$E:
$$ w^i = \dfrac{\Delta d^{i-1}}{(\Delta d^{i-1})^T (R^{i-1} - R^i)} $$Então, resolve-se: $ \Delta d^i = H_s^i \left[ F - P(d^i) \right]$
E, atualiza-se a solução com: $ d^{i+1} = d^i + \Delta d^i $
Método da Secante - O Algoritmo BFGS
INÍCIO:Definir a tolerância ($tol = 10^{-3}$), $i = 0$, $max_{iter} = 20$ e estimar $d = d^0$.
Calcular a matriz Jacobiana, ou rigidez tangente $ K_T^i $:
- Definir, inicialmente, que $ K_s^0 \equiv K_T^0 $;
- Se $ det(K_s^0) = 0 $, pare com mensagem de erro!
- Se não, calcule $ H_s^0 \equiv \left( K_s^0 \right)^{-1} $;
- Calcular $ P(d^0) $ e $ R^0 = F - P(d^0) $;
Continuação - O Algoritmo BFGS (iterações)
- Calcular o incremento da solução $ \Delta d^i = \left( H_s^{i-1} \right)^{-1} R(d^{i-1}) $, sendo $ R(d^{i-1}) = \left[ F - P(d^{i-1}) \right] $ e se $conv_d \leq tol_d$, cálculo completo!
- Atualizar a solução: $ d^{i} = d^{i-1} + \Delta d^i $;
- Calcular $ R(d^i) = F - P(d^i) $ e se $conv_F \leq tol_F$, cálculo completo!;
- Calcular $ \Delta R = R(d^{i-1}) - R(d^i) $;
- Calcular $ v^i = R(d^{i-1}) \left[ 1 - \dfrac{(\Delta d^{i-1})^T \Delta R} {(\Delta d^{i})^T R(d^{i-1})} \right] - R(d^i)$;
- Calcular $ w^i = \dfrac{\Delta d^{i-1}}{(\Delta d^{i-1})^T \Delta R} $;
- Atualizar a inversa: $ H_s^i = \left[ I + w^i (v^i)^T \right] H_s^{i-1} \left[ I + w^i (v^i)^T \right] $
- Definir: $ i = i + 1 $ e se $ i > max_{iter} $, pare com mensagem de erro!
- Ou então, voltar ao passo 1!
Método incremental da Força
- O método de Newton-Raphson converge rapidamente quando o estimador inicial está próximo da solução
- Na mecânica dos sólidos, normalmente, o estimador inicial refere-se à situação indeformada da estrutra
- Dificuldades de convergência ocorrem quando a força aplicada é grande*.
- Solução: aplicar as cargas em incrementos até atingir o valor total**.
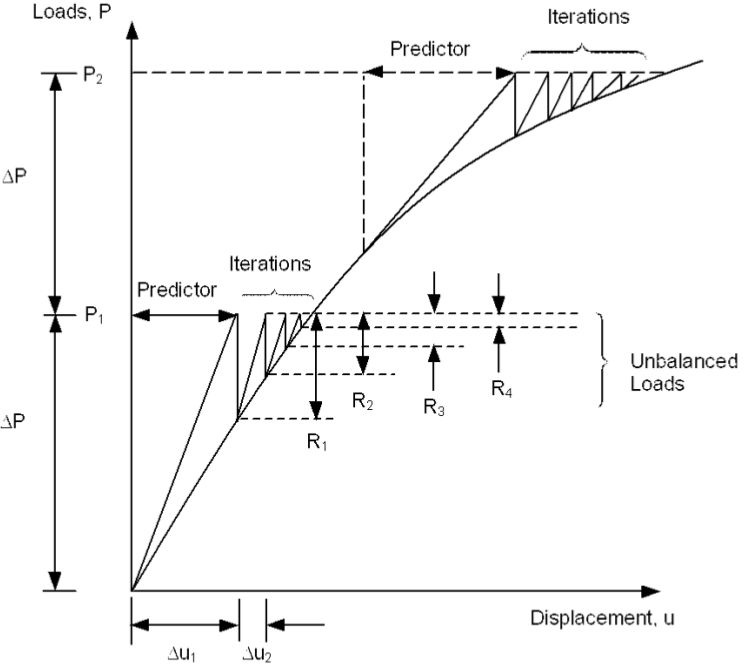
Método incremental da Força (cont. 1)
- Os incrementos de carregamento não precisam ser uniformes:
- Partes críticas precisam de incrementos menores*
- As soluções nos incrementos de força intermediários:
- O histórico da resposta pode fornecer informações sobre o problema;
- Podem estimar pontos de bifurcação ou a carga crítica;
- O incrementos de força afetam consideravelmente a precisão em problemas dependentes do caminho**.
- A melhor forma de verificar se o incremento de força está muito grande ou muito pequeno é contar o número de iterações para a convergência***.
Incrementos de Força X Deslocamentos
- Controle de forças: gradualmente aumentam-se as forças aplicadas e encontra-se a configuração de equilíbrio;
- Controle de deslocamentos: gradualmente aumentam-se os deslocamentos prescritos:
- A força aplicada pode ser calculada como uma reação;
- É mais estável que o controle das forças;
- Útil para contatos, "snap-through"...
Exercícios
Grafique a curva força-deslocamento usando Newton-Raphson, através
do aumento do deslocamento $ u_2 $ de 0 até 0,9 com 9 incrementos,
para as mesmas molas não lineares em série:

Rigidez das molas:
$$ k_1 = 50 + 500u $$ $$ k_2 = 100 + 200u $$Equações governantes:
$$ \begin{cases} 300u_1^2 + 400u_1u_2 - 200u_2^2 + 150u_1 - 100 u_2 = 0 \\ 200u_1^2 - 400u_1u_2 + 200u_2^2 - 100u_1 + 100 u_2 = 100 \end{cases} $$Passos para solução não linear
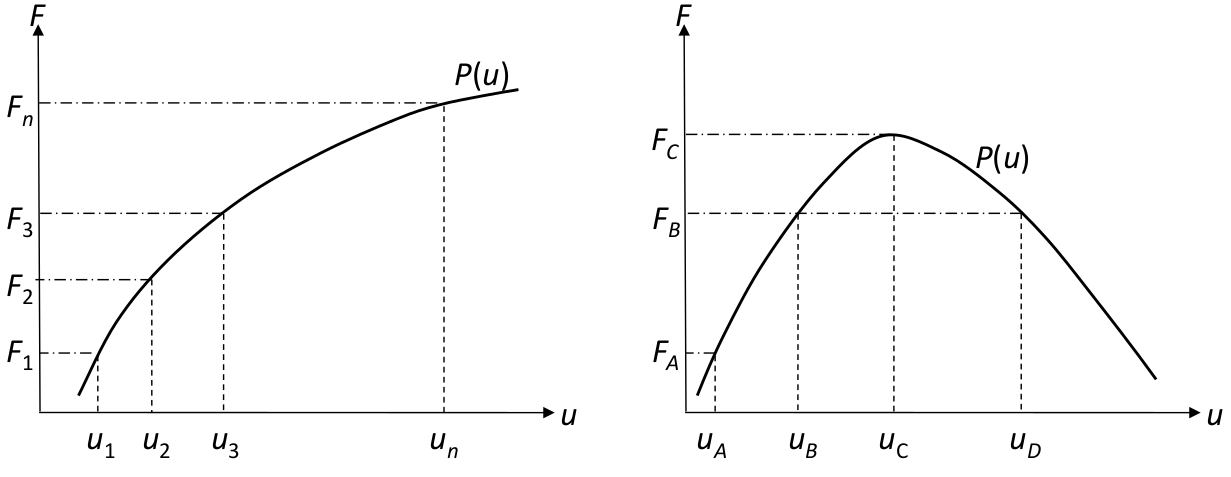
Passos para solução não linear
- Inicialização: $ d^0 = 0 $ e $ i = 0 $;
- Cálculo do resíduo: $ R^i = F - P(d^i) $;
- Verificação de convergência (se convergiu, pare!);
- Linearização
- Cálculo da matriz de rigidez tangente (ou matriz jacobiana): $ K_T^i(d^i) $;
- Solução Incremental:
- Resolver: $ K_T^i(d^i) \Delta d^i = R^i $
- Determinação do estado:
- Atualização de:
- Deslocamentos: $ d^{i+1} = d^i + \Delta d^i $
- Tensões: $ \sigma^{i+1} = \sigma^i + \Delta \sigma^i $
Passos para solução não linear (cont. 1)
- Cálculo do resíduo**:
- Forças nodais devido a tensões internas = - forças nodais aplicadas
- Determinação do estado:
- Para um dado deslocamento $ d^k $, determine o estado atual (deformações, tensões, etc)
- As vezes, tensões não podem ser determinadas usando somente as deformações!
Exemplo - Material Linear Elástico
Equação governante (equação escalar):
$$ \iiint_{\Omega} \varepsilon(\overline{u})^T \sigma d\Omega = \iint_{\Gamma_s} \overline{u}^T f^{\Gamma} d\Gamma + \iiint_{\Omega} \overline{u}^T f^b d\Omega $$Substituindo $ \overline{u} = N \overline{d} $ e $ \varepsilon(\overline{u}) = B \overline{d} $, e isolando $ \overline{d} $:
$$ \overline{d}^T \left( \underbrace{\iiint_{\Omega} B^T \sigma d\Omega}_{P(d)} = \underbrace{\iint_{\Gamma_s} N^T f^{\Gamma} d\Gamma + \iiint_{\Omega} N^T f^b d\Omega}_F \right)$$Exemplo - Material Linear Elástico (cont. 1)
O resíduo é:
$$ R = F - P(d) $$Material elastico linear:
$$ \sigma = D \varepsilon = D B d $$ $$ K_T = \dfrac{\partial P(d)}{\partial d} = \iiint_\Omega B^T D B d\Omega $$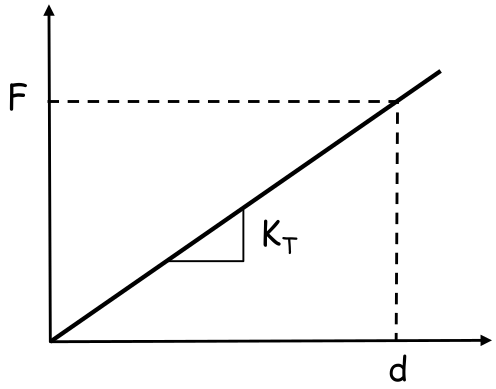
Exemplo - Material Não Linear (borracha)

Constantes do material:
$ E = 100 $ MPa
$ m = 40 $
$ A = 10^{-4} \ m^2 $
Relação tensão deformação da barra de borracha:
$$ \sigma = E tan^{-1}(m \varepsilon) $$Exemplo - Material Não Linear (cont. 1)
Forma fraca discreta: $ \overline{d}^T \int_0^L B^T \sigma A dx = \overline{d}^T F $
Sendo: $ B = \dfrac{1}{L} \left[ -1 \quad 1 \right] $ (barra)
Ou: $ B = \dfrac{1}{L} $ (restingido em $d_1$)
O resíduo é: $R = F - \int_0^L \dfrac{\sigma A}{L} dx $
ou seja: $ R = F - P(d) A $
Exemplo - Material Não Linear (cont. 2)
Jacobiano: $ \dfrac{dP}{dd} = \dfrac{d \sigma(d)}{dd} A = \dfrac{d\sigma}{d\varepsilon} \dfrac{d\varepsilon}{dd} A = \dfrac{1}{L} m A E \left( \dfrac{1}{1 + m^2 \varepsilon^2} \right)$
Sendo: $ \dfrac{d\sigma}{d\varepsilon} = E m \left( \dfrac{1}{1 + m^2 \varepsilon^2} \right) $ e: $ \dfrac{d\varepsilon}{dd} = \dfrac{1}{L}$*
Da relação tensão-deformação, pode-se escrever: $ \varepsilon = \dfrac{1}{m} tan \left(\dfrac{\sigma}{E}\right) $
Sabendo-se que: $1 + tan^2(u) = \dfrac{1}{cos^2(u)}$
Equação de Newton-Raphson: $ \left[ \dfrac{1}{L} m A E cos^2 \left( \dfrac{\sigma^k}{E} \right) \right] \Delta d^k = F - \sigma^k A$
Exemplo - Material Não Linear (cont. 3)
Estimador inicial: $ d^0 = 0 $
Iteração 1:
$$ \left[ \dfrac{1}{L} m A E cos^2 \left( \dfrac{\sigma^0}{E} \right) \right] \Delta d^0 = F - \sigma^0 A $$Iteração 2:
$$ \left[ \dfrac{1}{L} m A E cos^2 \left( \dfrac{\sigma^1}{E} \right) \right] \Delta d^1 = F - \sigma^1 A $$Newton-Raphson ou Newton-Raphson Modificado?
- É sempre recomendado utilizar métodos incrementais*:
- Não linearidade simples: $ \sim $ incrementos;
- Não linearidade complicada: $ 20 \sim 100 $ incrementos;
- Em cada incremento, Newton Raphson ou Newton Raphson modificado
pode ser utilizado:
- Newton Raphson calcula $ K_T $ a cada iteração;
- Newton Raphson modificado somente calcula $ K_T $ uma vez;
Newton-Raphson ou Newton-Raphson Modificado?
- Newton Raphson é melhor quando:
- A não linearidade é simples (leve);
- O critério de convergência mais rigoroso.
- Newton Raphson modificado é melhor quando:
- Cálculo computacional é custoso;
- Incremento pequeno;
- Newton Raphson não converge bem.
Precisão X Convergência
- O procedimento de solução não linear precisa de:
- Força interna $ P(d) $;
- Jacobiano ou matriz de rigidez tangente: $ K_T(d) = \dfrac{\partial P}{\partial d} $;
- Normalmente implementados na mesma rotina.
- A força interna necessita de precisão:
- Resolve-se o equilíbrio de $ P(d) = F $
- A matriz de rigidez tangente contribui para a convergência:
- $ K_T $ precisa fornece convergência quadratica;
- $ K_T $ aproximada necessita dae mais iterações;
- $ K_T $ errônea causa falta de convergência.
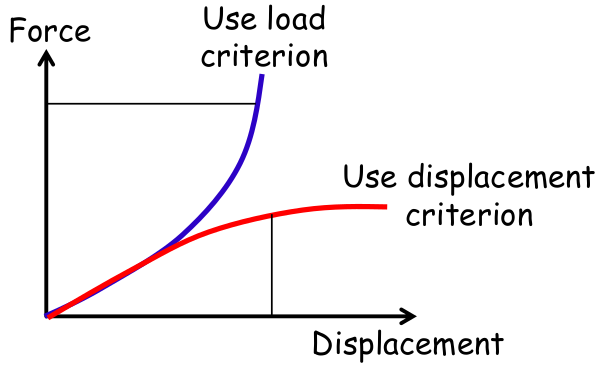
Critério de Convergência
- Normalmente são três:
- Trabalho, deslocamento e carregamento (residual);
- Trabalho = deslocamento * carregamento;
- Pelo menos dois critérios devem convergir.
- O critério de convergência tradicional é o de carregamento (residual):
- Equilíbrio entre forças internas e externas $ P(d) = F(d) $
- O critério de deslocamentos é utilizado para sistemas insensíveis ao tipo do carregamento.
Estratégias de Solução
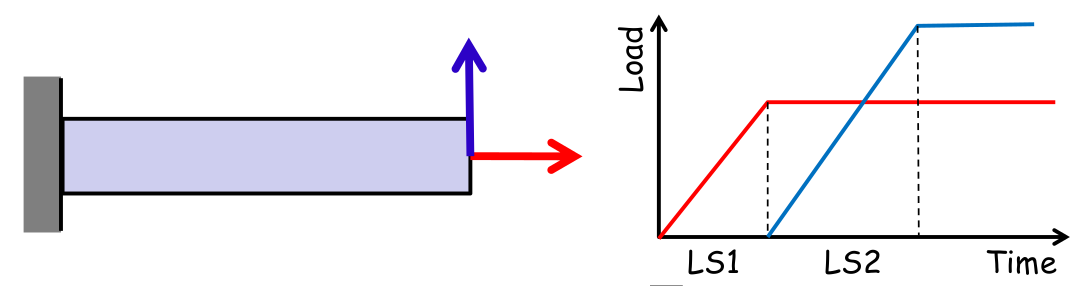
- Casos de carregamento (ou passos de carga)*:
- Um caso de carregamento é um conjunto de cargas e condições de contorno que definem um problema de análise;
- Múltiplos casos de carregamento pode ser utilizados para definir uma sequência de condições de carregamento:
Estratégias de Solução (cont. 1)
- Incrementos de carga*:
- Análise linear diz respeito à carga total;
- Análise não linear depende do caminho de carregamento (história);
- A carga aplicada é aumentada gradualmente em um passo de carga;
- Seguem o caminho da carga, melhoram a precisão e convergem facilmente.
Estratégias de Solução (cont. 2)
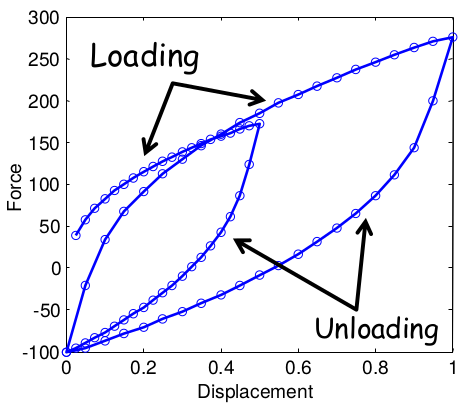
- Iteração de convergência:
- Dentro de um incremento de carga, um método iterativo* é utilizado para encontrar a solução não linear;
- Além disso, para tentar novamente a convergência antes da parada por máximas tentativas, métodos como da Bisecção, busca linear, estabilização, etc. podem ser utilizados.
Estratégias de Solução (cont. 3)
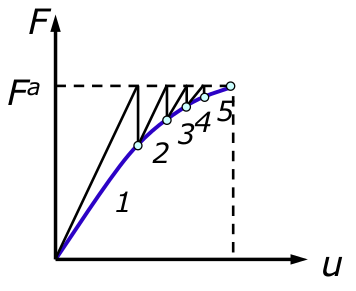
- Incremento de carga automático (variável)*:
- O incremento de carga pode não ser uniforme;
- Quando a iteração de convergência diverge, o incremento de carga é reduzido a metade;
- Se a solução convergir em menos de 4 iterações, aumenta-se o incremento em 25%;
- Se a solução converge em mais de 8 iterações, diminui-se o incremento em 25%.
- Subincremento**:
- Quando não há convergência em dado incremento, retorna-se ao anterior qua convergiu e reduz-se o incremento a metade;
- Processo repetido até o número máximo de subincrementos.
Quando a análise não linear não converge
- O método de Newton Raphson adota uma curvatura constante localmente;
- Quando o sinal da curvatura muda em torno da solução, o método de Newton Raphson oscila ou diverge;
- Geralmente a força residual muda de sinal entre iterações;
- Uma busca linear pode ajudar a convergir.
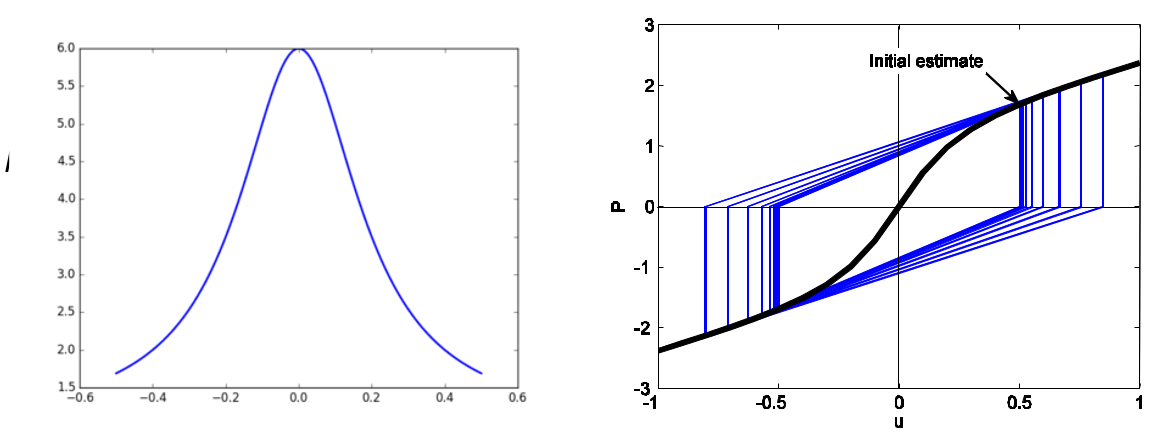 $$ P(d) = d + tan^{-1}(5d) $$
$$ \dfrac{d P}{d d} = 1 + 5cos^2(tan^{-1}(5d)) $$
$$ P(d) = d + tan^{-1}(5d) $$
$$ \dfrac{d P}{d d} = 1 + 5cos^2(tan^{-1}(5d)) $$
Quando a análise não linear não converge (cont. 1)
Procedimentos de Controle de deslocamento x Controle de força:
- Quase todos os problemas lineares são controlados por força;
- Procedimento de controle de deslocamento é mais estável para análises não lineares;
- Usa-se as reações para calcular as forças aplicadas.

Quando a análise não linear não converge (cont. 2)
Distorções na malha:
- A análise deve ser parada quando a malha está muito distorcida;
- Uma malha boa inicialmente pode ser distorcida durante um grande deslocamento;
- Exite a possibilidade de se utilizar procedimentos de remalhagem, mas ainda são inprecisos e inconvenientes;
- O melhor é fazer a malha de certo modo que a qualidade da mesma se preserve após os deslocamentos (tentativa e erro).
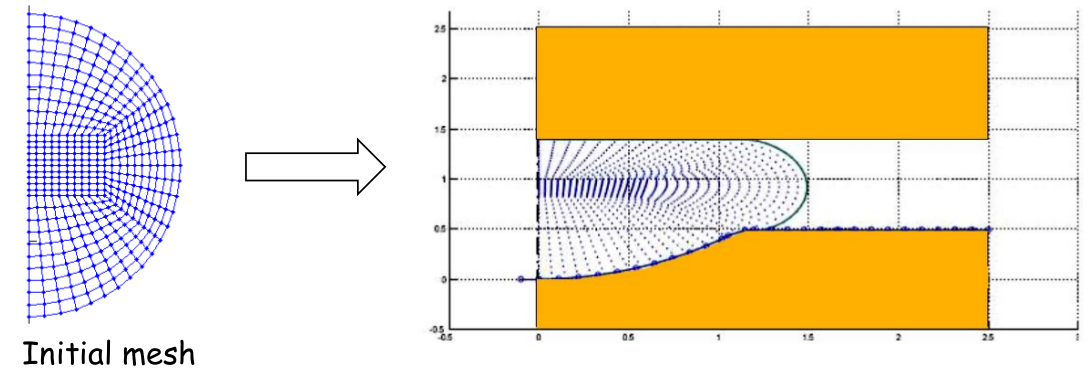
Exercício Final 1
Seja a barra da figura abaixo e sabendo que o módulo de elasticidade varia com a deformação:
$$ \sigma = E(u) \varepsilon (u) \quad \varepsilon (u) = \dfrac{du}{dx} \quad E(u) = E_0 \left( 1 - \dfrac{du}{dx} \right)$$Use um elemento para a barra e resolva o deslocamento da ponta da barra usando força incremental com 10 incrementos iguais.
Use $ E_0 = 1,0 GPa $, $ A = 10^{-4} $ e $ F = 25 kN $ e grafique a curva força x deslocamento.
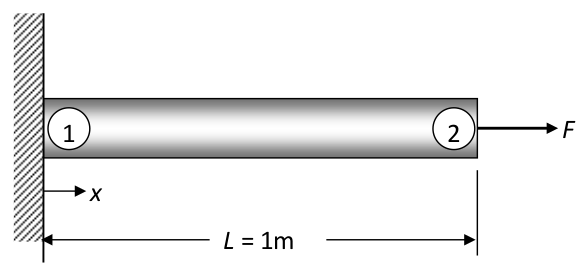
Exercício Final 2
A barra uniforme da figura abaixo apresenta comportamento elastoplástico conforme figura. A deformação plástica inicia em $ \sigma_y = 400 MPa $. Na região elástica $ E = 200 GPa $ e na plástica $ E_T = 20 GPa $. A barra tem $ A = 2e10^{-4} m^2 $ e $ L = 1,0 m $.
Calcule o deslocamento na ponta da barra quando uma força de $ F = 50 kN $ é aplicada na extremidade.
Grafique a curva força x deslocamento e adote relação deslocamento-deformação linear.

Elementos Finitos para análises não lineares elásticas
Relembrando conceitos...
- Problemas elásticos não lineares usam diferentes medidas de tensão e deformação função das modificações na geometria de referência;
- Deformação Lagrangiana é independente da rotação de corpo rígido, porém, deformações infinitesimais não;
- Qualquer deformação pode ser unicamente decomposta em rotação de corpo rígido e extensão*;
- O determinante do gradiente de deformação é relacionado com a mudança de volume, enquanto que o próprio gradiente de deformação e a normal a superfície estão relacionados com a mudança na área;
- Quatro diferente medições de tensão são definidas baseadas na geometria de referência;
- Quando a deformação é infinitesimal, todas as medições de tensões e deformações são idênticas;
Elementos Finitos para análises não lineares elásticas
- A equação variacional será obtida utilizando-se o princípio da energia potencial mínima*;
- O método de Newton-Raphson será utilizado (há a necessidade de cálculo da matriz jacobiana);
- Formulação Lagrangiana Total (material) usa a configuração indeformada como referência;
- Formulação Lagrangiana Atualizada (espacial) utiliza a configuração atual como referência;
- Ambas são matematicamente equivalentes, porém com diferentes aspectos computacionais.
Relação Constitutiva
Em materiais elásticos, a densidade de energia de deformação $ W $ existe, tal que, diferenciando-se a densidade de energia de deformação em relação às deformações adequadas, obtém-se as relacionadas tensões, por exemplo*:
$$ \textbf{S} = \dfrac{\partial W}{\partial \textbf{E}} $$Ou seja, é necessário, com essa formulação, expressar $ W $ em função de $ E $ e, no caso, manter a relação elástica linear**.
Para tal, pode-se utilizar o modelo de St. Venant-Kirchhoff***:
$$ W = \dfrac{1}{2} \textbf{E} : \textbf{D} : \textbf{E} $$Relação Constitutiva (cont. 1)
O tensor constitutivo de 4 ordem para materiais isotrópicos é:
$$ D_{ijkl} = \lambda \delta_{ij} \delta_{kl} + \mu (\delta_{ik} \delta_{jl} + \delta_{il} \delta_{jk}) $$ou
$$ \textbf{D} = \lambda \textbf{i} \otimes \textbf{i} + 2 \mu \textbf{I} $$E as constantes de Lamé:
$$ \lambda = \dfrac{\nu E}{(1 + \nu)(1 - 2\nu)} \quad \mu \equiv G = \dfrac{E}{2(1 + \nu)} $$Relação Constitutiva (cont. 2)
Portanto, para o modelo de St. Venant-Kirchhoff:
- Cálculo das tensões (diferenciando a densidade de energia de deformação): $$ \textbf{S} = \dfrac{\partial W}{\partial \textbf{E}} = \textbf{D} : \textbf{E} = \lambda \text{tr}(\textbf{E}) \textbf{i} + 2 \mu \textbf{E}$$
- Cálculo das deformações: $$ \textbf{E} = \dfrac{1}{2} \left( \textbf{C} - \textbf{i} \right) $$ Aplicando-se a decomposição polar: $$ \textbf{E} = \dfrac{1}{2} \left( \textbf{F}^T \textbf{F} - \textbf{i} \right) = \dfrac{1}{2} \left( \textbf{U}^2 - \textbf{i} \right)$$ Mostra que a rotação de corpo rígido não influência na deformação.
Condições de Contorno
As condições de contorno podem ser definidas como:
- Essencial (deslocamento no contorno): $$ \textbf{u} = \textbf{g} \quad \quad \text{em} \ \Gamma^h $$
- Natural (tração no contorno)*: $$ \textbf{t} = \textbf{P}^T \textbf{N} \quad \quad \text{em} \ \Gamma^s $$
Formulação Variacional
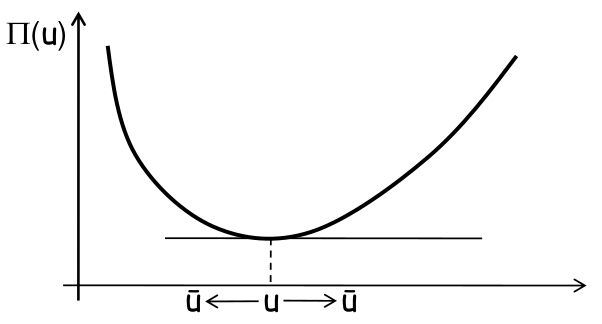
O objetivo é minimizar o potencial de energia para atingir o equilíbrio*.
$$ \Pi = \Pi^{int} + \Pi^{ext} $$ $$ \Pi = \iint_{\Omega_0} W d\Omega - \iint_{\Omega_0} \textbf{u}^T \textbf{f}^b d\Omega - \int_{\Gamma^S_0} \textbf{u}^T \textbf{t} $$Para tal, deve-se encontrar um $ \textbf{u} $ que minimize esse potencial de energia**:
- Perturba-se $ \textbf{u} $ em direção a $ \bar{\textbf{u}} $ proporcionalmente a $ \tau $;
- Se $ \textbf{u} $ minimiza o potencial de energia,$ \Pi $ deve ser menor que $ \Pi(\textbf{u}_{\tau}) $ para todo $ \bar{\textbf{u}} $ admissível.
Formulação Variacional (cont. 1)
Variação da energia potencial (derivada direcional):
$$ \bar{\Pi}(\textbf{u},\bar{\textbf{u}}) = \dfrac{d}{d\tau} \Pi(\textbf{u} + \tau \bar{\textbf{u}}) \Biggr\rvert_{\tau=0} $$- $ \Pi $ depende somente de $ \textbf{u} $, mas $ \bar{\Pi} $ depende de $ \textbf{u} $ e $ \bar{\textbf{u}} $;
- A energia potencial mínima acontece quando sua variação se torna zero para qualquer $ \bar{\textbf{u}} $ possível;
Exemplo unidimensional:
Formulação Variacional - Exemplo com mola linear
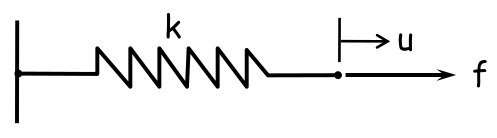
- Energia potencial: $ \Pi =\dfrac{1}{2} k \cdot u^2 - f \cdot u $
- Perturbação: $ \Pi(u + \tau \bar{u}) = \dfrac{1}{2} k \cdot (u + \tau \bar{u}) - f \cdot (u + \tau \bar{u}) $
- Diferenciação*: $ \dfrac{d}{d \tau} \left[ \Pi(u + \tau \bar{u}) \right] = k \cdot (u + \tau \bar{u}) \cdot \bar{u} - f \cdot \bar{u} $
- Avaliação no estado original: $ \dfrac{d}{d \tau} \left[ \Pi(u + \tau \bar{u}) \right] \biggr\rvert_{\tau=0} = k \cdot u \cdot \bar{u} - f \cdot \bar{u} = 0 $
Formulação Lagrangiana Total
Usando o método de Newton-Raphson com força incremental:
seja um sistema estático com $ N $ passos de carga, sendo $ n $ o passo atual da carga $ t $.
Assumindo que a solução convergiu em $ ^{n-1}t_k $ com $ k $ iterações, o objetivo é encontrar o equilíbrio do estado $ ^{n}t_{i} $, com $ i = 0 ... k $
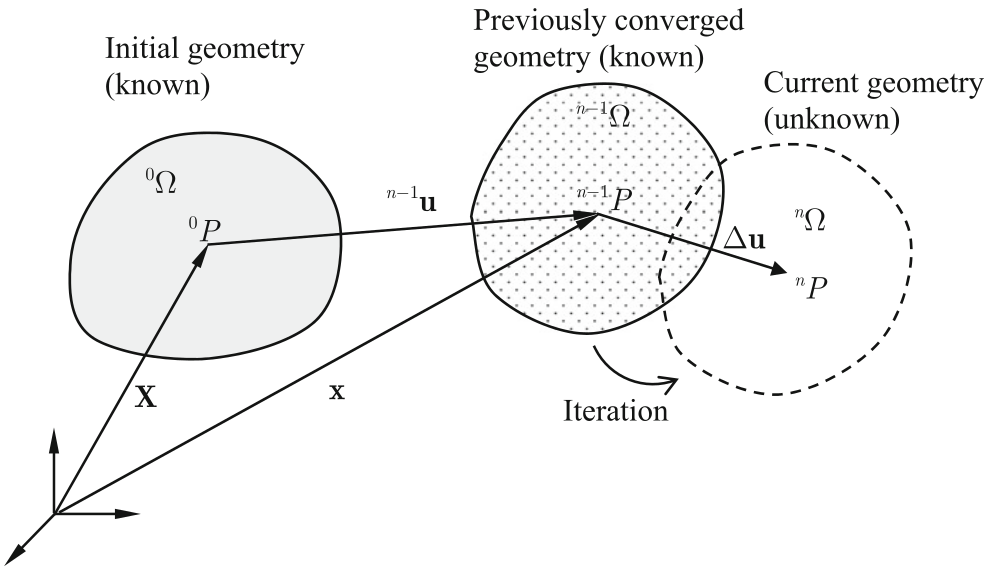
Formulação Lagrangiana Total (cont. 1)
Na formulação Total Lagrangiana:
- A configuração indeformada é a referência;
- Portanto, o segundo tensor de tensões de Piola-Kirchhoff $ S $ e a deformação Lagrangiana $ E $ são as escolhas naturais;
- Equação variacional:
$$ \bar{\Pi} = \iint_{\Omega_0} \dfrac{\partial W}{\partial \textbf{E}} : \bar{\textbf{E}} d\Omega
- \iint_{\Omega_0} \bar{\textbf{u}}^T \textbf{f}^b d\Omega
- \int_{\Gamma_o^S} \bar{\textbf{u}}^T \textbf{t} d\Gamma = 0$$
Substituindo a variação da energia na deformação:
$$ \iint_{\Omega_0} \textbf{S} : \bar{\textbf{E}} d\Omega = \iint_{\Omega_0} \bar{\textbf{u}}^T \textbf{f}^b d\Omega + \int_{\Gamma_o^S} \bar{\textbf{u}}^T \textbf{t} d\Gamma $$
Formulação Lagrangiana Total (cont. 2)
Expressando a variação de deformações:
$$ \textbf{E}(\textbf{u}) = \dfrac{1}{2} \left( \textbf{C} - \textbf{I} \right) = \dfrac{1}{2} \left( \nabla_0 \textbf{u} + \nabla_0 \textbf{u}^T + \nabla_0 \textbf{u}^T \nabla_0 \textbf{u} \right)$$ $$ \bar{\textbf{E}}(\textbf{u},\bar{\textbf{u}}) = \dfrac{d}{d \tau} \textbf{E} ( \textbf{u} + \tau \bar{\textbf{u}} ) \biggr\rvert_{\tau=0} = \dfrac{1}{2} \left( \nabla_0 \bar{\textbf{u}} + \nabla_0 \bar{\textbf{u}}^T + \nabla_0 \bar{\textbf{u}}^T \nabla_0 \textbf{u} + \nabla_0 \textbf{u}^T \nabla_0 \bar{\textbf{u}} \right)$$ $$ \therefore \bar{\textbf{E}}(\textbf{u},\bar{\textbf{u}}) = \dfrac{1}{2} \left( \textbf{F}^T \nabla_0 \bar{\textbf{u}} + \nabla_0 \bar{\textbf{u}}^T \textbf{F} \right)$$Formulação Lagrangiana Total (cont. 3)
Retornando à equação variacional e chamando de:
$$ \underbrace{\iint_{\Omega_0} \textbf{S} : \bar{\textbf{E}} d\Omega}_{a(\textbf{u},\bar{\textbf{u}})} = \underbrace{\iint_{\Omega_0} \bar{\textbf{u}}^T \textbf{f}^b d\Omega + \int_{\Gamma_o^S} \bar{\textbf{u}}^T \textbf{t} d\Gamma}_{\ell(\bar{\textbf{u}})} $$Sendo $ a(\textbf{u},\bar{\textbf{u}}) $ a forma de energia e $ \ell(\bar{\textbf{u}}) $ a forma de carga.
$$ a(\textbf{u},\bar{\textbf{u}}) = \ell(\bar{\textbf{u}}) $$- Linearidade nos termos de deformação no caso do uso do material de St. Venant-Kirchhoff;
- Linearidade também nos termos de $ \bar{\textbf{u}} $;
- Não linearidade nos termos de $ \textbf{u} $ por causa da relação não linear entre deslocamentos e deformações;
Formulação Lagrangiana Total - Linearização
Resíduo:
$$ R = a(\textbf{u}, \bar{\textbf{u}}) - \ell(\bar{\textbf{u}}) $$O objetivo é linearizar $ R $ na direção de $ \Delta \textbf{u} $:
- Assume-se que $ \textbf{u} $ é perturbado na direção de $ \Delta \textbf{u} $ usando a variável $ \tau $;
- Então, a linearização se torna: $$ L[R] = \dfrac{\partial R(\textbf{u} + \tau \Delta \textbf{u})}{\partial \tau}\biggr\rvert_{\tau=0} = \left[ \dfrac{\partial R}{\partial \textbf{u}} \right]^T \Delta \textbf{u}$$
- $ R $ é não linear em relação a $ \textbf{u} $, mas $ L[R] $ é linear em relação a $ \Delta \textbf{u} $;
- Supondo uma iteração $ k $ que não convergiu, o incremento de deslocamentos $ \Delta \textbf{u} $ é obtido fazendo-se o resíduo em $ k + 1 $ ser igual a zero: $$ R^{k+1} \approx \left[ \dfrac{\partial R^k}{\partial \textbf{u}} \right]^T \Delta \textbf{u} + R^k = 0$$
Formulação Lagrangiana Total - Linearização (cont. 1)
Que, basicamente, é o método de Newton-Raphson:
$$ \left[ \dfrac{\partial R^k}{\partial \textbf{u}} \right]^T \Delta \textbf{u} = - R^k$$E o estado atualizado:
$$ \textbf{u}^{k+1} = \textbf{u}^k + \Delta \textbf{u}^k $$ $$ \textbf{x}^{k+1} = \textbf{X} + \textbf{u}^{k+1} $$Sabe-se como calcular $ R $, e como variar $ R $ em $ \textbf{u} $?
$$ \dfrac{\partial}{\partial \textbf{u}}[R] = \dfrac{\partial}{\partial \textbf{u}}[a(\textbf{u}, \bar{\textbf{u}}) - \ell(\bar{\textbf{u}})] $$Note que o termo $ \ell(\bar{\textbf{u}}) $ desaparece caso não se considere a carga dependente do deslocamento*, ou seja:
- Somente a linearização da energia é necessária;
Formulação Lagrangiana Total - Linearização (cont. 2)
Linearização da energia:
$$ L[a(\textbf{u}, \bar{\textbf{u}})] = L \left[ \iint_{\Omega^0} \textbf{S} : \bar{\textbf{E}} d\Omega \right] = \iint_{\Omega_0} \left[ \Delta \textbf{S}:\bar{\textbf{E}} + \textbf{S} : \Delta \bar{\textbf{E}} \right] d\Omega $$- Observe que o domínio está fixado na indeformada!
- Precisa-se escrever em termos do incremento de deslocamento $ \Delta \textbf{u} $.
Incremento de Tensões (material de St. Venant-Kirchhoff):
$$ \Delta \textbf{S} = \dfrac{\partial S}{\partial E} : \Delta \textbf{E} = \textbf{D} : \Delta \textbf{E} $$Incremento de deformações (deformação de Green-Lagrange):
$$ \Delta \textbf{E} = \dfrac{1}{2}(\Delta \textbf{F}^T \textbf{F} + \textbf{F}^T \Delta \textbf{F}) $$ $$ \Delta \textbf{F} = \Delta \left( \dfrac{\partial \textbf{x}}{\partial \textbf{X}} \right) = \Delta \left( \dfrac{\partial (\textbf{X} + \textbf{u})}{\partial \textbf{X}} \right) = \dfrac{\partial \textbf{u}}{\partial \textbf{X}} = \nabla_0 \Delta \textbf{u} $$Formulação Lagrangiana Total - Linearização (cont. 3)
Continuação, incremento de deformações*:
$$ \Delta \textbf{E} = \dfrac{1}{2}(\Delta \textbf{F}^T \textbf{F} + \textbf{F}^T \Delta \textbf{F}) = \dfrac{1}{2}(\nabla_0 \Delta \textbf{u}^T \textbf{F} + \textbf{F}^T \nabla_0 \Delta \textbf{u})$$Variação do incremento de deformação**:
$$ \Delta \bar{\textbf{E}} = \Delta \left[ \dfrac{1}{2} \left( \textbf{F}^T \nabla_0 \bar{\textbf{u}} + \nabla_0 \bar{\textbf{u}}^T \textbf{F} \right) \right] = \dfrac{1}{2} \left( \Delta\textbf{F}^T \nabla_0 \bar{\textbf{u}} + \nabla_0 \bar{\textbf{u}}^T \Delta\textbf{F} \right) $$ $$ \therefore \Delta \bar{\textbf{E}} = \dfrac{1}{2} \left( \nabla_0 \Delta \textbf{u}^T \nabla_0 \bar{\textbf{u}} + \nabla_0 \bar{\textbf{u}}^T \nabla_0 \Delta \textbf{u} \right)$$Energia linearizada***:
$$ L[a(\textbf{u}, \bar{\textbf{u}})] = \iint_{\Omega^0} \left[ \bar{\textbf{E}} : \textbf{D} : \Delta \textbf{E} + \textbf{S} : \Delta \bar{\textbf{E}} \right] d\Omega \equiv a^{*}(\textbf{u} ; \Delta \textbf{u}, \bar{\textbf{u}}) $$Formulação Lagrangiana Total - Linearização (cont. 4)
Iteração de Newtow-Raphson com força incremental:
- Seja $ t_n $ o passo de carga atual e $ k + 1 $ a iteração atual;
- Então, o iteração de Newton-Raphson pode ser feira com: $$ a^{*}(^{n}\textbf{u}^k ; \Delta \textbf{u}^k, \bar{\textbf{u}}) = \ell(\bar{\textbf{u}}) - a(^{n}\textbf{u}^k, \bar{\textbf{u}}) $$
- O deslocamento total atualizado: $$ ^{n}\textbf{u}^{k+1} = ^{n}\textbf{u}^k + \Delta\textbf{u}^k $$
- Ou ainda, a iteração na forma discreta: $$ {\bar{\textbf{d}}}^T \left[ ^n\textbf{K}^k_T \right] {\Delta \textbf{d}^k} = {\bar{\textbf{d}}}^T { ^n\textbf{R}^k }$$
Quem são $ \left[ ^n\textbf{K}^k_T \right] $ e ${ ^n\textbf{R}^k } $?
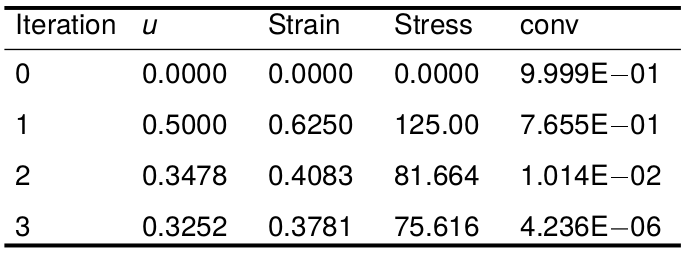
Formulação Lagrangiana Total - Exemplo
Seja a barra da figura abaixo, use um elemento para a barra e resolva o deslocamento da ponta da barra usando a formulação total lagrangiana.
Use $ E_0 = 200 Pa $, $ A = 1,0 m^2 $ e $ F = 100 kN $.

Resolver na mão até a linearização.
Formulação Lagrangiana Atualizada
A configuração atual (deformada) é a referência.
- Lembre-se: é desconhecida até o problema ser resolvido.
- Como integrar se não é conhecido o domínio de integração?
Quais medidas de tensão e deformação devem ser utilizadas?
- Tensão: tensor de tensão de Cauchy ($ \sigma $);
- Deformação: tensor de deformação de engenharia ($ \varepsilon $)*. Mas, deve ser definido na configuração atual (deformada): $$ \boldsymbol{\varepsilon} = \dfrac{1}{2} \left( \dfrac{\partial \textbf{u}}{\partial \textbf{x}}^T + \dfrac{\partial \textbf{u}}{\partial \textbf{x}} \right) $$
Formulação Lagrangiana Atualizada (cont. 1)
A equação variacional da formulação Lagrangiana Atualizada será derivada da formulação Lagrangiana Total.
A tensão de Cauchy se relaciona com o segundo tensor de Piola-Kirchhoff na forma:
$$ \boldsymbol{\sigma} = \dfrac{1}{J} \textbf{F} \textbf{S} \textbf{F}^T $$ $$ \textbf{S} = J \textbf{F}^{-1} \boldsymbol{\sigma} (\textbf{F}^{-1})^T $$A variação da deformação Lagrangiana é (definido anteriormente), e multiplicando corretamente por $ \textbf{F}^T $ e $ \textbf{F} $:
$$ \bar{\textbf{E}}(\textbf{u},\bar{\textbf{u}}) = \dfrac{1}{2} \left( \textbf{F}^T \nabla_0 \bar{\textbf{u}} + \nabla_0 \bar{\textbf{u}}^T \textbf{F} \right) = \dfrac{1}{2} \textbf{F}^T \left( (\textbf{F}^{-1})^T \nabla_0 \bar{\textbf{u}}^T + \nabla_0 \bar{\textbf{u}} \textbf{F}^{-1} \right) \textbf{F} $$ $$ \therefore \bar{\textbf{E}}(\textbf{u},\bar{\textbf{u}}) = \textbf{F}^T \bar{\boldsymbol{\varepsilon}} \textbf{F} \quad \text{ou} \quad \bar{\boldsymbol{\varepsilon}} = (\textbf{F}^{-1})^T \bar{\textbf{E}} \textbf{F}^{-1}$$De forma similar:
$$ \Delta \textbf{E}(\textbf{u},\bar{\textbf{u}}) = \textbf{F}^T \Delta \boldsymbol{\varepsilon} \textbf{F} \quad \text{com:} \quad \Delta \boldsymbol{\varepsilon} = \dfrac{1}{2} \left( \dfrac{\partial \Delta \textbf{u}}{\partial \textbf{x}}^T + \dfrac{\partial \Delta \textbf{u}}{\partial \textbf{x}} \right) $$Formulação Lagrangiana Atualizada (cont. 2)
A forma de energia é transformada, então:
$$ \iint_{\Omega_0} \textbf{S} : \bar{\textbf{E}} d\Omega = \iint_{\Omega_0} J \textbf{F}^{-1} \boldsymbol{\sigma} (\textbf{F}^{-1})^T : \textbf{F}^T \bar{\boldsymbol{\varepsilon}} \textbf{F} d\Omega = \iint_{\Omega_0} \boldsymbol{\sigma} : \bar{\boldsymbol{\varepsilon}} J d\Omega = \iint_{\Omega_X} \boldsymbol{\sigma} : \bar{\boldsymbol{\varepsilon}} d\Omega $$O que demonstra que as formas material e espacial são matematicamente equivalentes.
$$ \therefore a_X(\textbf{u}, \bar{\textbf{u}}) = \iint_{\Omega_X} \boldsymbol{\sigma} : \bar{\boldsymbol{\varepsilon}} d\Omega $$O que acontece com o termo de carga $ \ell(\bar{\textbf{u}}) $?
Formulação Lagrangiana Atualizada - Linearização
A linearização de $ a_X(\textbf{u}, \bar{\textbf{u}}) $ é complexa pois não se conhece a configuração atual (deformada é função de $ \textbf{u} $).
De maneira similar a forma de energia, pode-se converter a forma de energia lineariza da formulação Lagrangiana total, sendo essa:
$$ a^{*}(\textbf{u} ; \Delta \textbf{u}, \bar{\textbf{u}}) = \iint_{\Omega^0} \left[ \bar{\textbf{E}} : \textbf{D} : \Delta \textbf{E} + \textbf{S} : \Delta \bar{\textbf{E}} \right] d\Omega $$O termo de rigidez inicial convertido:
$$ \textbf{S} : \Delta \bar{\textbf{E}} = J \textbf{F}^{-1} \boldsymbol{\sigma} (\textbf{F}^{-1})^T : \dfrac{1}{2} \left( \nabla_0 \Delta \textbf{u}^T \nabla_0 \bar{\textbf{u}} + \nabla_0 \bar{\textbf{u}}^T \nabla_0 \Delta \textbf{u} \right) $$ $$ = J F^{-1}_{ik} \sigma_{kl} F^{-1}_{jl} \dfrac{1}{2} \left( \dfrac{\partial \bar{u}_m}{\partial X_i} \dfrac{\partial \Delta u_m}{\partial X_j} + \dfrac{\partial \Delta u_m}{\partial X_i} \dfrac{\partial \bar{u}_m}{\partial X_j} \right) \equiv J \sigma_{kl} \underbrace{\dfrac{1}{2} \left( \dfrac{\partial \bar{u}_m}{\partial x_k} \dfrac{\partial \Delta u_m}{\partial x_l} + \dfrac{\partial \Delta u_m}{\partial x_k} \dfrac{\partial \bar{u}_m}{\partial x_l} \right)}_{\boldsymbol{\eta} (\Delta \textbf{u}, \bar{\textbf{u}})}$$Formulação Lagrangiana Atualizada - Linearização (cont. 1)
Ou seja, o termo de rigidez inicial:
$$ \textbf{S} : \Delta \bar{\textbf{E}} = J \boldsymbol{\sigma} : \boldsymbol{\eta}(\Delta \textbf{u}, \bar{\textbf{u}}) $$O termo de rigidez tangente convertido:
$$ \bar{\textbf{E}} : \textbf{D} : \Delta \textbf{E} = (\textbf{F}^T \bar{\boldsymbol{\varepsilon}} \textbf{F}) : \textbf{D} : (\textbf{F}^T \Delta \boldsymbol{\varepsilon} \textbf{F}) = F_{ki} \bar{\varepsilon}_{kl} F_{lj} D_{ijmn} F_{pm} \Delta \varepsilon_{pq} F_{qn}$$ $$ = J \bar{\varepsilon}_{kl} \underbrace{\left[ \dfrac{1}{J} F_{ki} F_{lj} D_{ijmn} F_{pm} F_{qn} \right]}_{\text{Tensor constitutivo espacial de $4^a$ ordem}} \Delta \varepsilon_{pq} $$Ou seja, o termo de rigidez tangente:
$$ \bar{\textbf{E}} : \textbf{D} : \Delta \textbf{E} = J \bar{\boldsymbol{\varepsilon}} : \textbf{c} : \Delta \boldsymbol{\varepsilon}$$Sendo: $ c_{ijkl} = \dfrac{1}{J} F_{ir} F_{js} F_{km} F_{ln} D_{rsmn} $
Formulação Lagrangiana Atualizada - Linearização (cont. 2)
Portanto a forma linearizada da formulação Lagrangiana atualizada:
$$ a^{*} (\textbf{u} ; \Delta \textbf{u}, \bar{\textbf{u}}) = \iint_{\Omega^0} \left[ \bar{\boldsymbol{\varepsilon}} : \textbf{c} : \Delta \boldsymbol{\varepsilon} + \boldsymbol{\sigma} : \boldsymbol{\eta} (\Delta \textbf{u}, \bar{\textbf{u}}) \right] J d\Omega $$ $$ a^{*}_X (\textbf{u} ; \Delta \textbf{u}, \bar{\textbf{u}}) = \iint_{\Omega^X} \left[ \bar{\boldsymbol{\varepsilon}} : \textbf{c} : \Delta \boldsymbol{\varepsilon} + \boldsymbol{\sigma} : \boldsymbol{\eta} (\Delta \textbf{u}, \bar{\textbf{u}}) \right] d\Omega$$Iteração de Newton-Raphson:
$$ a^{*} (^n\textbf{u}^k ; \Delta \textbf{u}^k, \bar{\textbf{u}}) = \ell(\bar{\textbf{u}}) - a(^n\textbf{u}^k, \bar{\textbf{u}}) $$Observações:
- Ambas formulações são idênticas teoricamente, porém com diferentes expressões;
- A implementação numérica será diferente;
- A relação constitutiva também é diferente.
Tensor constitutivo espacial
Sendo o material de St. Venanr-Kirchhoff:
$$ \textbf{D} = \lambda \textbf{i} \otimes \textbf{i} + 2 \mu \textbf{I} $$ou
$$ D_{ijkl} = \lambda \delta_{ij} \delta_{kl} + \mu (\delta_{ik} \delta_{jl} + \delta_{il} \delta_{jk}) $$Utilizando a relação com o tensor de deformação esquerdo de Cauchy-Green $ \text{G} = \textbf{F}\textbf{F}^T $, chega-se a:
$$ c_{ijkl} = \dfrac{1}{J} \left[ \lambda G_{ij} G_{kl} + \mu (G_{ik} G_{jl} + G_{il} G_{jk}) \right]$$Observações:
- $ \textbf{D} $ é constante, mas $ \textbf{c} $ não;
- $ \textbf{S} = \textbf{D} : \textbf{E} $ mas $ \boldsymbol{\sigma} \neq \textbf{c} : \boldsymbol{\varepsilon} $
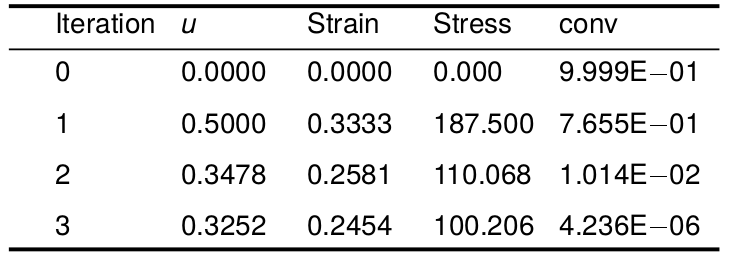
Formulação Lagrangiana Atualizada - Exemplo
Seja a barra da figura abaixo, use um elemento para a barra e resolva o deslocamento da ponta da barra usando a formulação total lagrangiana.
Use $ E_0 = 200 Pa $, $ A = 1,0 m^2 $ e $ F = 100 kN $.

Resolver na mão até a linearização.
Formulação de Elementos Finitos para Elasticidade não linear
Conceitos Iniciais:
- Será utilizada a notação de Voigt:
- Tensor de segunda ordem $ \rightarrow $ vetor;
- Tensor de quarta ordem $ \rightarrow $ matriz
- Vetores de tensão e deformação, exemplo*: $$ \textbf{S} = \{S_{11} \ S_{22} \ S_{12} \}^T $$ $$ \textbf{E} = \{E_{11} \ E_{22} \ 2E_{12} \}^T $$
- O tensor constitutivo utilizando-se o material isotrópico linear de St. Venant-Kirchhoff para o exemplo bidimensional: $$ \textbf{D} = \lambda \textbf{i} \otimes \textbf{i} + 2 \mu \textbf{I} = \left[ \begin{array}{ccc} D_{1111} & D_{1122} & D_{1112} \\ D_{2211} & D_{2222} & D_{2212} \\ D_{1211} & D_{1222} & D_{1212} \end{array} \right] $$
Elemento e formulação geométrica não linear
Inicialmente será discutido o elemento do estado plano de deformação, quadrilateral de 4 nós, utilizando a formulação lagrangiana total.
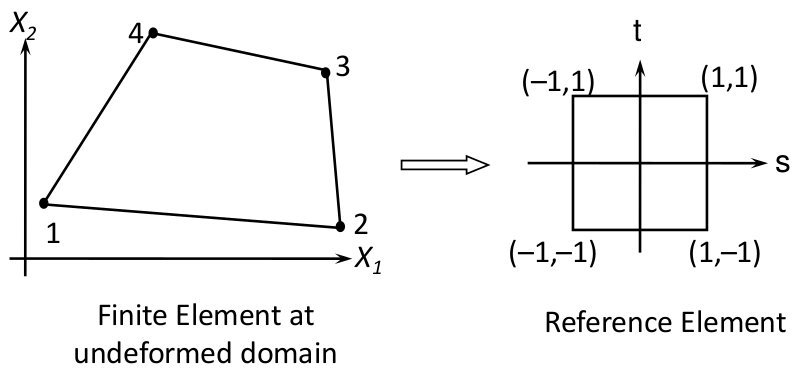
Interpolação e Mapeamento Isoparamétrico
- Interpolação dos deslocamentos* ($n$ = o nó, $n_n$ = número total de nós): $$ \textbf{u} = \sum^{n_{n}}_{n=1} N_{n}(\boldsymbol{\xi}) \textbf{u}_{n} $$
- Mapeamento Isoparamétrico**:
$$ \textbf{X} = \sum^{n_{n}}_{n=1} N_{n}(\boldsymbol{\xi}) \textbf{X}_{n} $$
- A mesma função de interpolação é utilizada para o mapeamento da geometria.
- Funções de interpolação para o elemento quadrilateral de 4 nós do slide anterior:
Gradientes de deslocamento e deformação
- Gradiente de deslocamento:
$$ \dfrac{\partial \textbf{u}}{\partial \textbf{X}} = \sum^{n_n}_{n=1}
\dfrac{\partial N_n(\boldsymbol{\xi})}{\partial \textbf{X}} \textbf{u}_n \quad
\text{com} \quad u_{i,j} = \sum^{n_n}_{n=1} N_{n,j}(\boldsymbol{\xi}) u_{n,i}$$
$$ \nabla_0 \textbf{u} = \{u_{1,1} \ u_{1,2} \ u_{2,1} \ u_{2,2}\}^T $$
- Como calcular $ \dfrac{\partial N_n(\boldsymbol{\xi})}{\partial \textbf{X}} $?
- Gradiente de deformação: $$ \textbf{F} = \textbf{I} + \nabla_0 \textbf{u} = \{ F_{11} \ F_{12} \ F_{21} \ F_{22} \}^T = \{ 1 + u_{1,1} \ u_{1,2} \ u_{2,1} \ 1 + u_{2,2} \}^T$$
AMBOS gradientes de deslocamento e de deformação são assimétricos!
Deformação Lagrangiana
$$ \textbf{E} = \dfrac{1}{2}(\textbf{C} - \textbf{I}) = \dfrac{1}{2}\left( \nabla_0 \textbf{u} + \nabla_0 \textbf{u}^T + \nabla_0 \textbf{u}^T \nabla_0 \textbf{u} \right) $$ $$ \therefore \textbf{E} = \left\lbrace \begin{array}{c} E_{11} \\ E_{22} \\ 2E_{12} \end{array} \right\rbrace = \left\lbrace \begin{array}{c} u_{1,1} + \dfrac{1}{2}(u_{1,1}u_{1,1} + u_{2,1}u_{2,1}) \\ u_{2,2} + \dfrac{1}{2}(u_{1,2}u_{2,1} + u_{2,2}u_{2,2}) \\ u_{1,2} + u_{2,1} + u_{1,2}u_{1,1} + u_{2,1}u_{2,2} \end{array} \right\rbrace$$- Devido a não linearidade: $ \textbf{E} \neq \textbf{B} \textbf{u} $
Para o material de St. Venant-Kirchhoff:
$$ \textbf{D} = \lambda \textbf{i} \otimes \textbf{i} + 2 \mu \textbf{I} = \left[ \begin{array}{ccc} \lambda + 2 \mu & \lambda & 0 \\ \lambda & \lambda + 2 \mu & 0 \\ 0 & 0 & \mu \end{array} \right]$$Variação da Deformação Lagrangiana
Embora $\textbf(E)$ seja não linear, $\bar{\textbf{E}}$ é linear
$$ \bar{\textbf{E}} = \dfrac{1}{2} \left( \textbf{F}^T \nabla_0 \bar{\textbf{u}} + \nabla_0 \bar{\textbf{u}}^T \textbf{F} \right) \quad \longrightarrow \quad \bar{\textbf{E}} = \textbf{B}_{NL} \bar{\textbf{u}}$$$$ \textbf{B}_{NL} = \left[ \begin{array}{cccccccc} F_{11}N_{1,1} & F_{21}N_{1,1} & F_{11}N_{2,1} & F_{21}N_{2,1} & F_{11}N_{3,1} & F_{21}N_{3,1} & F_{11}N_{4,1} & F_{21}N_{4,1} \\ F_{12}N_{1,2} & F_{22}N_{1,2} & F_{12}N_{2,2} & F_{22}N_{2,2} & F_{12}N_{3,2} & F_{22}N_{3,2} & F_{12}N_{4,2} & F_{22}N_{4,2} \\ {F_{12}N_{1,1} + \\ + F_{11}N_{1,2}} & {F_{21}N_{1,2} + \\ + F_{22}N_{1,1}} & {F_{12}N_{2,1} + \\ + F_{11}N_{2,2}} & {F_{21}N_{2,2} + \\ + F_{22}N_{2,1}} & {F_{12}N_{3,1} + \\ + F_{11}N_{3,2}} & {F_{21}N_{3,2} + \\ + F_{22}N_{3,1}} & {F_{12}N_{4,1} + \\ + F_{11}N_{4,2}} & {F_{21}N_{4,2} + \\ + F_{22}N_{4,1}} \end{array} \right] $$
$$ \bar{\textbf{u}} = \{\bar{u}_{11} \ \bar{u}_{12} \ \bar{u}_{21} \ \bar{u}_{22} \ \bar{u}_{31} \ \bar{u}_{32} \ \bar{u}_{41} \ \bar{u}_{42}\}^T $$Equação Variacional
- Forma de Energia: $$ a(\textbf{u}, \bar{\textbf{u}}) = \iint_{\Omega_0} \textbf{S} : \bar{\textbf{E}} d\Omega $$ $$ a(\textbf{u}, \bar{\textbf{u}}) \approx \bar{\textbf{u}}^T \iint_{\Omega_0} \textbf{B}_{NL}^T \textbf{S} d\Omega$$ $$ a(\textbf{u}, \bar{\textbf{u}}) \equiv \bar{\textbf{u}}^T F^{int}$$
- Forma de Força: $$\ell(\bar{\textbf{u}}) = \iint_{\Omega_0} \bar{\textbf{u}}^T \textbf{f}^b d\Omega + \iint_{\Gamma^s_0} \bar{\textbf{u}}^T \textbf{t} d\Gamma $$ $$ \ell(\bar{\textbf{u}}) \approx \sum_{n=1}^{n_e} \bar{\textbf{u}}_n^T \left[ \iint_{\Omega_0} N_n(\boldsymbol{\xi}) \textbf{f}^b d\Omega + \iint_{\Gamma^s_0} N_n(\boldsymbol{\xi}) \textbf{t} d\Gamma \right] $$ $$ \ell(\bar{\textbf{u}}) \equiv \bar{\textbf{u}}^T F^{ext} $$
- Resíduo: $$ \bar{\textbf{u}}^T F^{int} = \bar{\textbf{u}}^T F^{ext} $$
Linearização
- Incremento de deformação*: $ \Delta \textbf{E} = \textbf{B}_{NL} \Delta \textbf{u} $
- Variação do incremento de deformação: $$ \Delta \bar{\textbf{E}} = \dfrac{1}{2} \left( \nabla_0 \Delta \textbf{u}^T \nabla_0 \bar{\textbf{u}} + \nabla_0 \bar{\textbf{u}}^T \nabla_0 \Delta \textbf{u} \right)$$
- Linearização: $$ \iint_{\Omega_0} = \bar{\textbf{E}} : \textbf{D} : \Delta \textbf{E} d\Omega = \bar{\textbf{u}}^T \left[ \iint_{\Omega_0} \textbf{B}_{NL}^T \textbf{D} \textbf{B}_{NL} d\Omega \right] \Delta \textbf{u} $$ $$ \iint_{\Omega_0} \textbf{S} : \Delta \bar{\textbf{E}} = \bar{\textbf{u}}^T \left[ \iint_{\Omega_0} \textbf{B}_{L}^T \textbf{S}_{\oslash} \textbf{B}_{L} d\Omega \right] \Delta \textbf{u}$$
Linearização (cont. 1)
Sendo:
$$ \textbf{S}_{\oslash} = \left[ \begin{array}{cccc} S_{11} & S_{12} & 0 & 0 \\ S_{21} & S_{22} & 0 & 0 \\ 0 & 0 & S_{11} & S_{12} \\ 0 & 0 & S_{21} & S_{22} \end{array} \right] $$ $$ \textbf{B}_{L} = \left[ \begin{array}{cccccccc} N_{1,1} & 0 & N_{2,1} & 0 & N_{3,1} & 0 & N_{4,1} & 0 \\ N_{1,2} & 0 & N_{2,2} & 0 & N_{3,2} & 0 & N_{4,2} & 0 \\ 0 & N_{1,1} & 0 & N_{2,1} & 0 & N_{3,1} & 0 & N_{4,1} \\ 0 & N_{1,2} & 0 & N_{2,2} & 0 & N_{3,2} & 0 & N_{4,2} \end{array} \right] $$Linearização (cont. 3)
- Rigidez: $$ \textbf{K} = \iint_{\Omega_0} \textbf{B}_{NL}^T \textbf{D} \textbf{B}_{NL} + \textbf{B}_{L}^T \textbf{S}_{\oslash} \textbf{B}_{L} d\Omega $$
- Equação incremental discreta (Newton-Raphson): $$ \bar{\textbf{u}}^T \textbf{K} \Delta \textbf{u} = \bar{\textbf{u}}^T (\textbf{F}^{ext} - \textbf{F}^{int})$$
- $ \textbf{K} $ muda de acordo com tensões e deformações;
- Resolução iterativa até o resíduo satisfazer a tolerância.
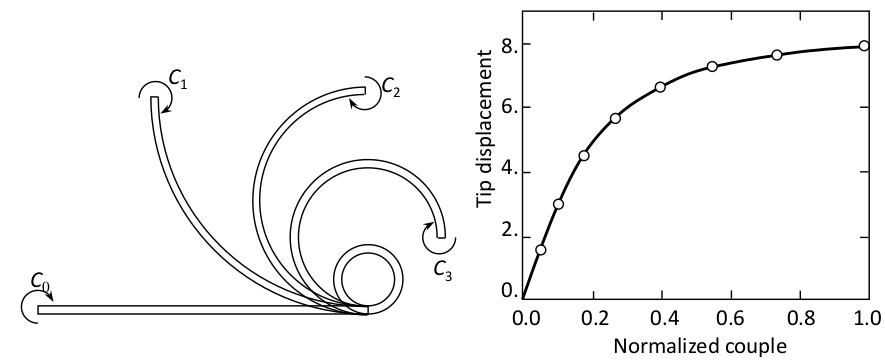
Exemplo não linearidade geométrica com elementos finitos
Grande deformação de uma viga em balanço.
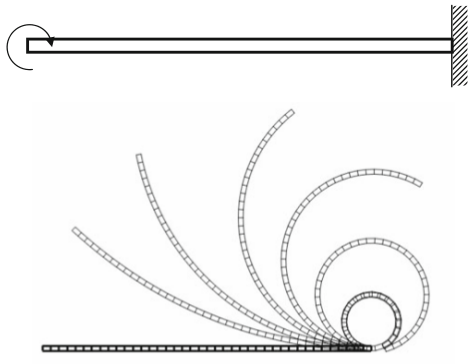
Dados:
- $ l_0 $ = 10 m;
- $ A $ = 100 x 147,8 mm (b x h);
- $ E_e $ = 100 MPa;
- $ M $ = 3384,78 N.m (na extremidade livre).
Resolver usando a formulação Lagrangiana Total e o método de Newton-Raphson.
Usar elemento do estado plano de tensões e elemento de viga de Euler-Bernoulli.
Graficar a deformada da viga a cada incremento de carga, a variação dos deslocamentos horizontal e vertical e a rotação na extremidade da viga.
Click it and the menu will open from the side.
Click anywhere on the slide to return to the presentation,
or use the close button in the menu.
If you don't like the menu button,
you can use the slide number instead.
Go on, give it a go.
The menu button can be hidden using the options,
but you need to enable the slide number link.
Or you can open the menu by pressing the m key.
You can navigate the menu with the keyboard as well.
Just use the arrow keys and <space> or <enter> to change slides.
You can disable the keyboard for the
menu in the options if you wish.
Left or Right
You can configure the menu to slide in from the left or right
Markers
The slide markers in the menu can be useful to show
you the progress through the presentation.
You can hide them if you want.
You can also add slide numbers.
Slide Titles
The menu uses the first heading to label each slide
but you can specify another label if you want.
Use a data-menu-title attribute in the section element to give the slide a custom label,
or add a menu-title class to any element in the slide you wish.
You can change the titleSelector option and use
any elements you like as the default for labelling each slide.
Vertical Slides
The menu indents your vertical slides so it's easy to see the structure of your presentation.

Next slide down
At the bottom

Themes
The menu can also be used to change the
theme of your presentation.
Just click the Themes button at the top of the menu.
The list of themes can be configured in the options.
Transitions
You can also change the default
transition style from the menu.
Of course,
if you don't want to see the Themes or Transitions menus you can hide them in the options.
Custom Panels
Create your own custom menu panels where
you can add your own html content.
Custom panels support menu items so you
can create your own menus that look and
behaviour just like the other menus.
Speaker View
The menu works independently in the speaker view.
You can changes slides without your audience
seeing you doing any of it.
THE END
Download reveal.js-menu and add it to your plugin folder
Have a look at the source code & documentation
And don't forget to check out Reveal.js if you haven't already